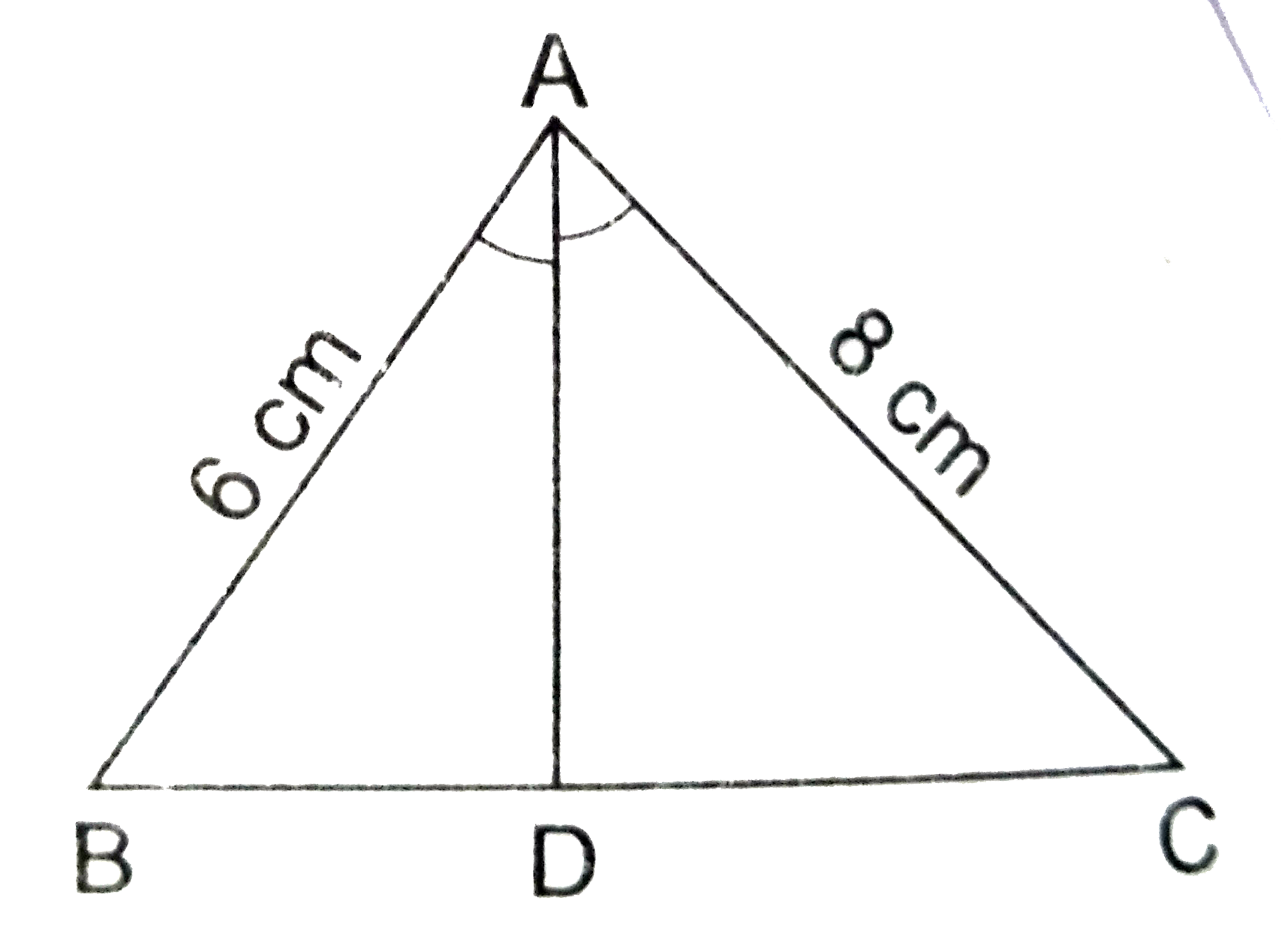
An isosceles triangle is symmetrical about the bisector of the angle included between the equal sides. In Fig. 3, △ABC is given in which AB =AC and AD is the bisector of ∠BACThen, AD is the line of symmetry of △ABC.true or false?
Step by step video & image solution for An isosceles triangle is symmetrical about the bisector of the angle included between the equal sides. In Fig. 3, triangle ABC is given in which AB =AC and AD is the bisector of angle BACThen, AD is the line of symmetry of triangle ABC.true or false? by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- REFLECTION AND ROTATIONAL SYMMETRYBOOK - RS AGGARWALCHAPTER - REFLECTION AND ROTATIONAL SYMMETRYEXERCISE - Exercise A(MCQ)
10 Videos
- REFLECTION AND ROTATIONAL SYMMETRYBOOK - RS AGGARWALCHAPTER - REFLECTION AND ROTATIONAL SYMMETRYEXERCISE - Exercise A(True / False)
7 Videos
- RATIONAL NUMBERSBOOK - RS AGGARWALCHAPTER - RATIONAL NUMBERSEXERCISE - TEST PAPER -(4)
17 Videos
- SIMPLE INTEREST BOOK - RS AGGARWALCHAPTER - SIMPLE INTEREST EXERCISE - test perper 12 D
1 Video
Similar Questions
Knowledge Check
In a triangle, with usual notations, the length of the bisector of angle A is
A2bcb+csinA2B2bcb+ccosA2Cabc2R(b+c)cosecA2D4Ab+ccosecA2In a △ABC. AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
A25:49B49:25C6:1D5:7In the adjoining figure, if ABC is a triangle in which AD is the bisector of ∠A. If AD⊥BC, then
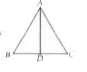 AΔABC is an isosceles triangleBΔABC is an equilateral triangleCΔABC is an scalene triangleDBD = AC
AΔABC is an isosceles triangleBΔABC is an equilateral triangleCΔABC is an scalene triangleDBD = AC
In the following figure, ∠ABC=90∘,AD=15 and DC=20.If BD is the bisector of ∠ABC, What is the perimeter of the triangle ABC?

View SolutionIf in a triangle ABC,CD is the angular bisector of the angle ACB then CD is equal to
View SolutionIn triangle ABC, AB = 6, AC = 7 and BC = 8. If AD is bisector of angleA , then find the length of BD and CD.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
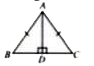
AD bisects ∠A
View SolutionIn a ΔABC,AD is the bisector of the angle A meeting BC at D. If I is the in centre of the triangle, then AI:DI is equal to
View Solution