Let ABCD be an isosceles trapezium in which AB||DC and AD=BC. Let E and F be the midpoints of AB and DC respectively.Then trap.ABCD symmetrical about EF.true or false?
To determine whether trapezium ABCD is symmetrical about line EF, we can follow these steps:
1. Understanding the Properties of the Trapezium:
- We have an isosceles trapezium ABCD where AB is parallel to DC (AB || DC) and the lengths of the non-parallel sides are equal (AD = BC).
2. Identifying the Midpoints:
- Let E be the midpoint of AB and F be the midpoint of DC. This means that AE = EB and DF = FC.
3. Drawing the Trapezium:
- Draw trapezium ABCD with AB at the top and DC at the bottom, ensuring that AB is parallel to DC. Mark points A, B, C, and D appropriately.
4. Drawing the Midpoints:
- Mark points E and F on line segments AB and DC respectively, ensuring that E and F are exactly halfway between the endpoints of their respective segments.
5. Analyzing Symmetry:
- A figure is symmetrical about a line if the line divides the figure into two identical halves.
- In this case, line EF divides the trapezium into two parts: triangle ABE and triangle CDF on one side, and triangle BEC and triangle DAF on the other side.
6. Conclusion:
- Since the lengths of AD and BC are equal and angles ABE and CDF are equal (due to the properties of isosceles trapezium), triangles ABE and CDF are congruent. Similarly, triangles BEC and DAF are also congruent.
- Therefore, trapezium ABCD is symmetrical about line EF.
Final Answer:
The statement is True.
---
- We have an isosceles trapezium ABCD where AB is parallel to DC (AB || DC) and the lengths of the non-parallel sides are equal (AD = BC).
- Let E be the midpoint of AB and F be the midpoint of DC. This means that AE = EB and DF = FC.
- Draw trapezium ABCD with AB at the top and DC at the bottom, ensuring that AB is parallel to DC. Mark points A, B, C, and D appropriately.
- Mark points E and F on line segments AB and DC respectively, ensuring that E and F are exactly halfway between the endpoints of their respective segments.
- A figure is symmetrical about a line if the line divides the figure into two identical halves.
- In this case, line EF divides the trapezium into two parts: triangle ABE and triangle CDF on one side, and triangle BEC and triangle DAF on the other side.
- Since the lengths of AD and BC are equal and angles ABE and CDF are equal (due to the properties of isosceles trapezium), triangles ABE and CDF are congruent. Similarly, triangles BEC and DAF are also congruent.
- Therefore, trapezium ABCD is symmetrical about line EF.
The statement is True.
Topper's Solved these Questions
- REFLECTION AND ROTATIONAL SYMMETRYBOOK - RS AGGARWALCHAPTER - REFLECTION AND ROTATIONAL SYMMETRYEXERCISE - Exercise A(MCQ)
10 Videos
- REFLECTION AND ROTATIONAL SYMMETRYBOOK - RS AGGARWALCHAPTER - REFLECTION AND ROTATIONAL SYMMETRYEXERCISE - Exercise A(True / False)
7 Videos
- RATIONAL NUMBERSBOOK - RS AGGARWALCHAPTER - RATIONAL NUMBERSEXERCISE - TEST PAPER -(4)
17 Videos
- SIMPLE INTEREST BOOK - RS AGGARWALCHAPTER - SIMPLE INTEREST EXERCISE - test perper 12 D
1 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2ABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
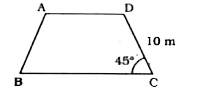 A10√2mB4√2mC5√2mD6√2m
A10√2mB4√2mC5√2mD6√2mABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=A40 cmB50 cmC60 cmD30 cm
Let ABCD be a kite in which AB =AD and BC=DC.Then, kite ABCD is symmetrical about the diagonal AC .true or false?
View SolutionABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
View SolutionABCD is a trapezium in which AB∣∣DC ∠A=∠B=30degree. Find ∠C and ∠D. Are these angles equal?

View SolutionABCD is a trapezium in which AB || DC, AB = 16 cm and DC = 24 cm. If E and Fare respectively the midpoints of AD and BC, prove that ar(ABFE) = 911 ar(EFCD).
View SolutionIn the given figure ABCD is a trapezium in which AB∣∣DC and AB:DC=3:2, The ratio of the areas of △AOB and △COD is
View Solution


