Question

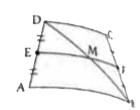
ABCD is a trapezium . AB ||CD and $AB:CD=5:4$, E and F are mid points of AD and BC, if CD= 20 cm , Find EF

Answer

`19 : 17`

Explanation

To find the length of EF in trapezium ABCD where AB || CD and the ratio AB:CD = 5:4, and given that CD = 20 cm, we can follow these steps:

Step 1: Understand the Ratio
The ratio of AB to CD is given as 5:4. This means that if we let the length of AB be 5x and the length of CD be 4x, we can express both lengths in terms of a variable x.

Step 2: Find the Value of x
Given that CD = 20 cm, we can set up the equation:
\( 4x = 20 \)
To find x, we divide both sides by 4:
\( x = \frac{20}{4} = 5 \)

Step 3: Calculate the Length of AB
Now that we have the value of x, we can find the length of AB:
\( AB = 5x = 5 \times 5 = 25 \text{ cm} \)

Step 4: Use the Midpoint Theorem
In a trapezium, the line segment joining the midpoints of the non-parallel sides (EF in this case) is given by the formula:
\( EF = \frac{AB + CD}{2} \)

Step 5: Substitute the Values
Now we can substitute the values of AB and CD into the formula:
\( EF = \frac{25 \text{ cm} + 20 \text{ cm}}{2} \)

Step 6: Calculate EF
Now, we perform the addition and division:
\( EF = \frac{45 \text{ cm}}{2} = 22.5 \text{ cm} \)

Final Answer
Thus, the length of EF is:
\( EF = 22.5 \text{ cm} \)

---