The area of a square ABCD is 36cm2. Find the area of the square obtained by joining the midpoints of the sides of the square ABCD.
17 cm2
18 cm2
28 cm2
10 cm2
The correct Answer is:B
To solve the problem step by step, we will follow these instructions:
Step 1: Find the side length of square ABCD.
Given that the area of square ABCD is 36cm2, we can use the formula for the area of a square, which is:
Area=side2
Let the side length of the square be a. Then we have:
a2=36
To find a, we take the square root of both sides:
a=√36=6cm
Step 2: Determine the midpoints of the sides of square ABCD.
The midpoints of the sides of square ABCD will be:
- Midpoint of side AB: P
- Midpoint of side BC: Q
- Midpoint of side CD: R
- Midpoint of side DA: S
Step 3: Calculate the length of the sides of the new square PQRS.
The distance between the midpoints P and Q (which forms one side of the new square) can be calculated as follows:
Since P and Q are midpoints of sides of length 6cm, the distance PQ is half the length of the side of square ABCD:
PQ=12×6=3cm
Step 4: Find the area of square PQRS.
Now, we can find the area of square PQRS using the formula for the area of a square:
Area of PQRS=side2
The side length of square PQRS is PQ, which we found to be 3cm:
Area of PQRS=32=9cm2
Final Answer:
The area of the square obtained by joining the midpoints of the sides of square ABCD is 9cm2.
---
Given that the area of square ABCD is 36cm2, we can use the formula for the area of a square, which is:
The midpoints of the sides of square ABCD will be:
- Midpoint of side BC: Q
- Midpoint of side CD: R
- Midpoint of side DA: S
The distance between the midpoints P and Q (which forms one side of the new square) can be calculated as follows:
Now, we can find the area of square PQRS using the formula for the area of a square:
The area of the square obtained by joining the midpoints of the sides of square ABCD is 9cm2.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20A20videos
MENSURATION
- BOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20B16videos
MENSURATION
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 1311videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - PERCENTAGE EXERCISE - TEST PAPER16videos
PERCENTAGE
Similar Questions
The diagonal of a square is 4√2cm. The diagonal of another square whose area is double that of the first square is :
View SolutionArea of a square ABCD is 16 cm, then find the area of the square formed by joining the middle points of the sides of this square.Acircle has been drawn around a rectangle of sides 6 cm and 8 cm, then find the area of the region inside the circle and outside
View SolutionFind the area of a square whose side is 5cm.
View SolutionFind the areas of the squares whose sides are :
10 cmView SolutionFind the areas of the squares whose sides are :
14 cmView SolutionThe area of square ABCD is 144 cm2 and the area of square PQRS is 81 cm2 and the area of square PQRS is 81 cm2, find the ratio of the side AB to the side PQ.
View SolutionThe area of square DEFG is 64 cm2 and the area of square WXYZ is 36 cm2, find the ratio of the perimeter of square DEFG to the perimeter of square WXYZ.
View SolutionFind the area of the triangle inscribed in a circle circumscribed by a square made by joining the midpoints of the adjacents sides of a square of side x?
View SolutionWhat is the area of the square ABCD shown in the diagram ?
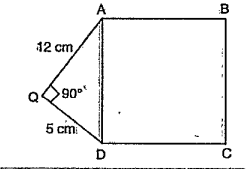 View Solution
View SolutionABCD is a square. Find out the side of square?
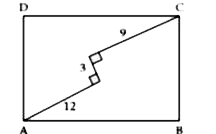 View Solution
View Solution

