Find the area of the triangle inscribed in a circle circumscribed by a square made by joining the midpoints of the adjacents sides of a square of side x?
3x216
3√3x232
34x2(π−12)
3√3x28
To find the area of the triangle inscribed in a circle that is circumscribed by a square formed by joining the midpoints of the adjacent sides of a square of side x, we can follow these steps:
Step 1: Understand the Geometry
We start with a square of side x. The midpoints of the adjacent sides of this square form another square, which will be the one circumscribing the circle.
Step 2: Determine the Side Length of the Inner Square
The distance between the midpoints of adjacent sides of the original square is given by:
AG=AH=x2
Thus, the side length of the square formed by these midpoints is:
GH=√(x2)2+(x2)2=√x24+x24=√x22=x√2
Step 3: Calculate the Diameter and Radius of the Circumscribed Circle
The diameter of the circle is equal to the length of the diagonal of the inner square:
Diameter=GH=x√2
Thus, the radius r of the circle is:
r=Diameter2=x2√2
Step 4: Find the Area of the Triangle Inscribed in the Circle
We know that the area of an equilateral triangle inscribed in a circle can be calculated using the formula:
Area=34r2√3
Substituting the radius we found:
Area=34(x2√2)2√3
Calculating r2:
r2=(x2√2)2=x28
Thus, the area becomes:
Area=34⋅x28⋅√3=3√3x232
Step 5: Final Area of the Triangle
Since the triangle is inscribed in the circle, the area of the triangle inscribed is three times the area of triangle formed by any two points on the circle and the center of the circle. Therefore, the final area of the triangle inscribed in the circle is:
Area=3⋅3√3x232=9√3x232
Conclusion
The area of the triangle inscribed in the circle is:
9√3x232
We start with a square of side x. The midpoints of the adjacent sides of this square form another square, which will be the one circumscribing the circle.
The distance between the midpoints of adjacent sides of the original square is given by:
AG=AH=x2
Thus, the side length of the square formed by these midpoints is:
GH=√(x2)2+(x2)2=√x24+x24=√x22=x√2
The diameter of the circle is equal to the length of the diagonal of the inner square:
Diameter=GH=x√2
Thus, the radius r of the circle is:
r=Diameter2=x2√2
We know that the area of an equilateral triangle inscribed in a circle can be calculated using the formula:
Area=34r2√3
Substituting the radius we found:
Area=34(x2√2)2√3
Calculating r2:
r2=(x2√2)2=x28
Thus, the area becomes:
Area=34⋅x28⋅√3=3√3x232
Since the triangle is inscribed in the circle, the area of the triangle inscribed is three times the area of triangle formed by any two points on the circle and the center of the circle. Therefore, the final area of the triangle inscribed in the circle is:
Area=3⋅3√3x232=9√3x232
The area of the triangle inscribed in the circle is:
9√3x232
Topper's Solved these Questions
Similar Questions
Knowledge Check
The area of a square ABCD is 36cm2. Find the area of the square obtained by joining the midpoints of the sides of the square ABCD.
A17 cm2B18 cm2C28 cm2D10 cm2The area of the circle that can be inscribed in a square of side 6 cm is
A36πcm2B18πcm2C12πcm2D9πcm2The area of a circle that can be inscribed in a square of side 6 cm is :
A36 πcm2B18 πcm2C12 πcm2D9 πcm2
The area of the circle that can be inscribed in a square of side 6 cm is
View SolutionWhat is the area of a circle inscribed in a square of side 'a' units?
View Solution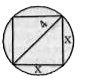
A square of side x is inscribed in a circle of radius 4 cm. Then x is
View SolutionWhat is the area of a circle which can be inscribed in a square of side 8 cm ?
View SolutionFind the ratio of the areas of squares circumscribed about and inscribed in the same circle.
View Solution
