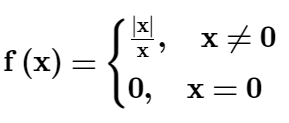Question

Evaluate:
${\displaystyle {\left(\text{lim}\right)}_{x\to 0}{\left(\frac{a^x+b^x+c^x}{3}\right)}^{\frac{2}{x}};(a,b,c>0)}$

Explanation

To evaluate the limit

$$\underset{x\to 0}{lim}{\left(\frac{a^x+b^x+c^x}{3}\right)}^{\frac{2}{x}},(a,b,c>0)$$

we can follow these steps:

Step 1: Identify the form of the limit
First, we substitute \( x = 0 \) into the expression:

\( \frac{a^0 + b^0 + c^0}{3} = \frac{1 + 1 + 1}{3} = 1. \)

Thus, we have:

\( \lim_{x \to 0} \left( \frac{a^x + b^x + c^x}{3} \right)^{\frac{2}{x}} = 1^{\infty}, \)

which is an indeterminate form.

Step 2: Rewrite the limit
To resolve the indeterminate form \( 1^{\infty} \), we can use the exponential limit property. We rewrite the limit as:

\( \lim_{x \to 0} \left( \frac{a^x + b^x + c^x}{3} \right)^{\frac{2}{x}} = e^{\lim_{x \to 0} \frac{2}{x} \left( \frac{a^x + b^x + c^x}{3} - 1 \right)}. \)

Step 3: Simplify the expression inside the limit
Now, we need to find:

\( \lim_{x \to 0} \frac{2}{x} \left( \frac{a^x + b^x + c^x}{3} - 1 \right). \)

Using the fact that \( a^x \approx 1 + x \log a \) as \( x \to 0 \), we can expand \( a^x, b^x, c^x \):

\( a^x \approx 1 + x \log a, \quad b^x \approx 1 + x \log b, \quad c^x \approx 1 + x \log c. \)

Thus,

\( a^x + b^x + c^x \approx 3 + x(\log a + \log b + \log c). \)

Now substituting this back into our limit gives:

\( \frac{a^x + b^x + c^x}{3} \approx 1 + \frac{x(\log a + \log b + \log c)}{3}. \)

Step 4: Substitute back into the limit
Now we have:

\( \frac{a^x + b^x + c^x}{3} - 1 \approx \frac{x(\log a + \log b + \log c)}{3}. \)

Thus, we can write:

\( \lim_{x \to 0} \frac{2}{x} \left( \frac{a^x + b^x + c^x}{3} - 1 \right) \approx \lim_{x \to 0} \frac{2}{x} \cdot \frac{x(\log a + \log b + \log c)}{3} = \lim_{x \to 0} \frac{2(\log a + \log b + \log c)}{3} = \frac{2(\log a + \log b + \log c)}{3}. \)

Step 5: Final limit evaluation
Now substituting this back into the exponential limit gives:

\( \lim_{x \to 0} \left( \frac{a^x + b^x + c^x}{3} \right)^{\frac{2}{x}} = e^{\frac{2(\log a + \log b + \log c)}{3}}. \)

Using the property of logarithms, we can simplify this to:

\( = e^{\log \left( (abc)^{\frac{2}{3}} \right)} = (abc)^{\frac{2}{3}}. \)

Final Answer
Thus, the limit evaluates to:

\( \lim_{x \to 0} \left( \frac{a^x + b^x + c^x}{3} \right)^{\frac{2}{x}} = (abc)^{\frac{2}{3}}. \)