A particle move with a velocity v=αt3 along a straight line.The average velocity in time interval t=0 to t=T is (A) αT3 (B) αT32 (C) αT33 (D) αT34
Step by step video & image solution for A particle move with a velocity v=alpha t^(3) along a straight line.The average velocity in time interval t=0 to t=T is (A) alphaT^(3) (B) (alpha T^(3))/(2) (C) (alpha T^(3))/(3) (D) (alpha T^(3))/(4) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A particle moves with a velocity v(t)=(12)kt2 along a straight line . Find the average speed of the particle in a time t.
View SolutionFigure shows the velocity time graph for a particle travelling along a straight line. The magnitude of average velocity (in m/s) of particle during the time interval from t=0 to t=6s is 10α. Find the value of α.
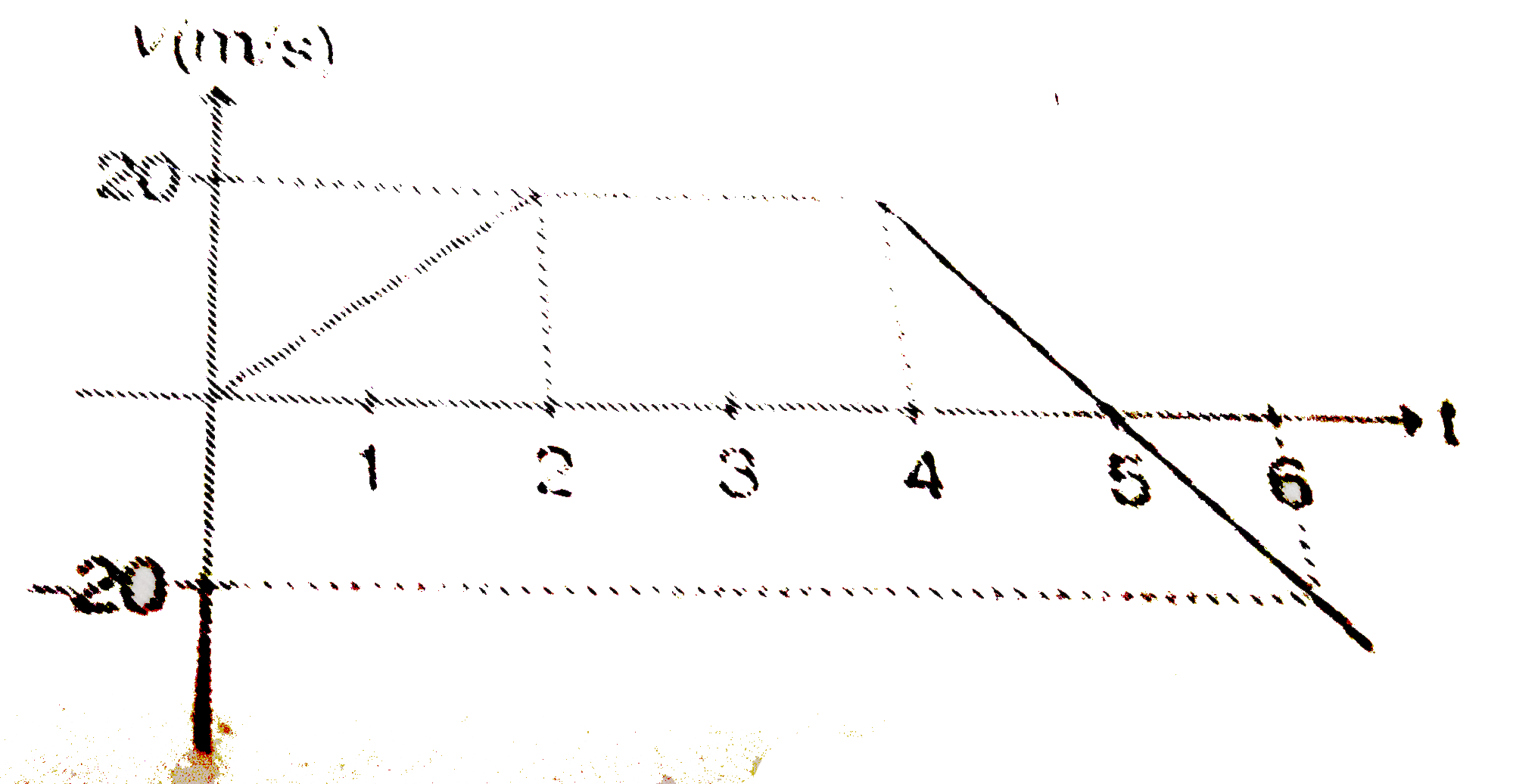 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle moves with an initial velocity v0 and retardation αv, where v is the velocity at any time t.
AThe particle will cover a total distance v0αBthe particle will come to rest after time 1αCthe particle will continue to move for a along timeDThe velocity of particle will become v0e after time 1α - Question 2 - Select One
A particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
Av2−v1t1−t2Bv2−v1t1+t2Cv2−t1t2−t1Dv1+v2t1−t2 - Question 3 - Select One
A particle is moving with velocity v=4t3+3t2−1m/s.
The displacement of particle in time t=1s to t=2s will beA21 mB17 mC13 mD9 m
A particle moves in a straight line as s=α(t−4)+β(t−4)2. Find the initial velocity and acceleration.
View SolutionA particle moves along a line by s=t3−9t2+24t then S is decreasing whent∈
View SolutionIf a particle is moving the velocity v(t)=cos πt, along a straight line such that at t=0, s=4, its position function is given by
View SolutionFor which of the following graphs the average velocity of a particl moving along a straight line for time interval (0,t) must be negative−
View SolutionThe position of a particle moving on a straight line depends on time t as
x=(t+3)sin(2t)View Solution
