From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 is hollwed out. Find the volume of the remaining solid.

Video Solution

Text Solution

Verified by Experts

Given that , side of a solid cube (a) = 7 cm
Height of conical cavity i.e., cone h = 7 cm

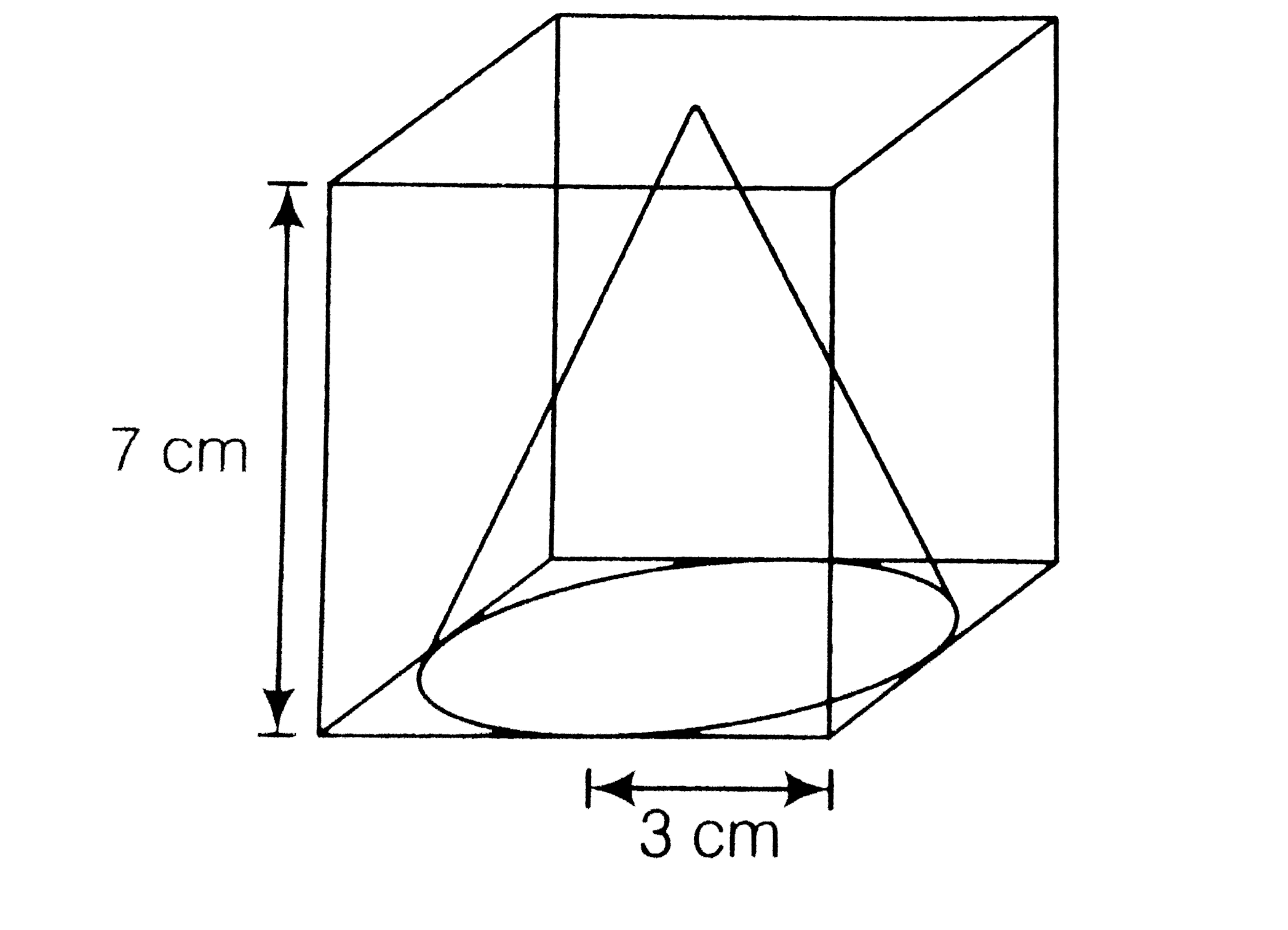
Since, the height of conical cavity and the sode of cube is equal that means the conical cavity fit vertically in the cube.
Radius of conical cavity i.e., cone ,r =3 cm
$\Rightarrow$ " "Diameter $= 2 \times r = 2 \times 3 = 6 c m$
Since, the diameter is less than the side of a cube that means the base of a conical cavity is
not fit inhorizatal of cube .
Now, volume of cube $= {(s id e)}^{3} = a^{3} = (7) = 343 c m^{3}$
and volume of conical cavity i.e., cone $= \frac{1}{3} π \times r^{2} \times h$
$= \frac{1}{3} \times \frac{22}{7} \times 3 \times 3 \times 7$
$= 66 c m^{3}$
$∴$ Volume of remainig soild = Volume of cube - Volume of conical cavity
$= 343 - 66 = 277 c m^{3}$
Hence, the required volume of solid is $277 c m^{3}$ .

Updated on:21/07/2023