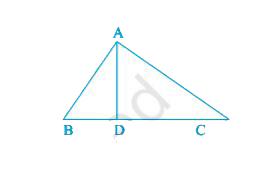
In figure, if ∠BAC=90∘ and AD⊥BC. Then,

A
BD.CD=BC2
B
AB⋅AC=BC2
C
BD⋅CD=AD2
D
AB⋅AC=AD2
Video Solution
Text Solution
The correct Answer is:C
Ib ΔADB and ΔADC,
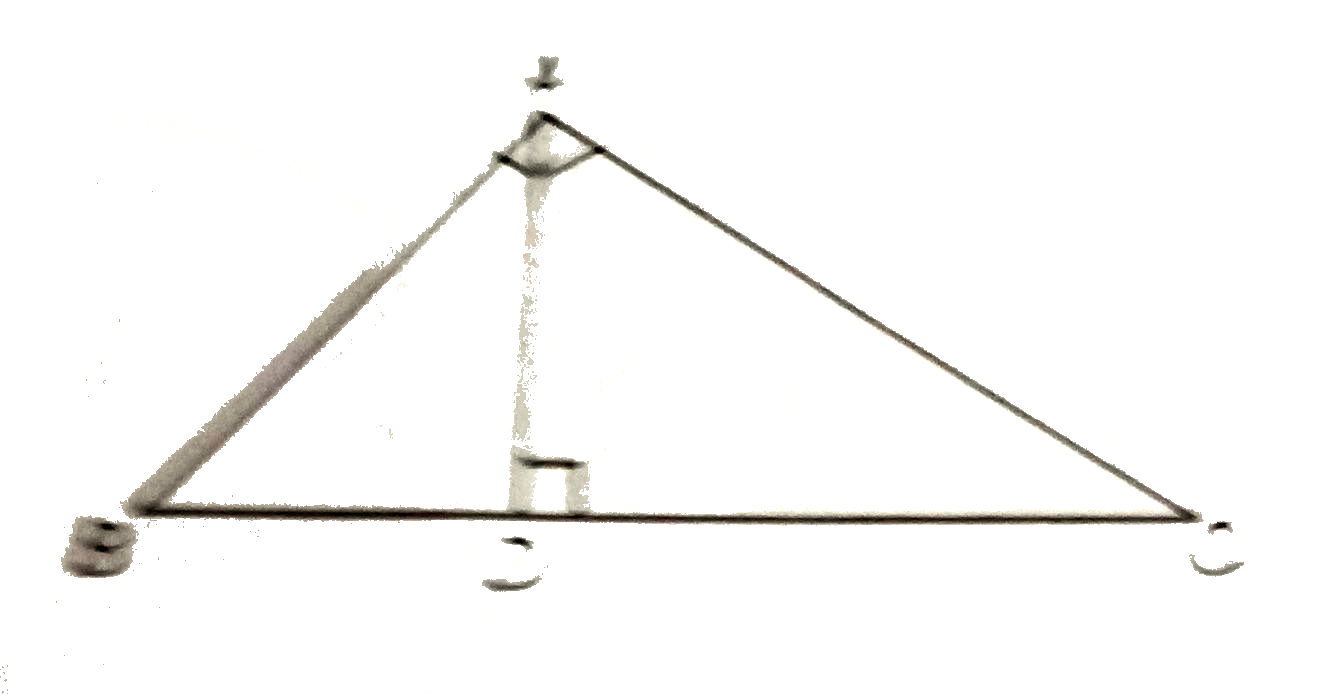
∠d=∠D=90∘
∠DBA=∠DAC [each equal to 90∘−<C]
∴ΔADB~ΔADC [by AAAsimilarity criterion]
∴BDAD=ADCD
⇒BD⋅CD=AD2
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, if ∠BAC=90∘ and AD⊥BC, then:
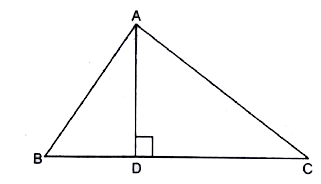 ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2
ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2In the figure given below ∠BAC=90∘ and AD ⊥ BC. Then
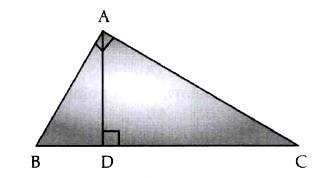 ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2
ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2In figure, if ∠AOB=90∘and∠ABC=30∘, then∠CAO is equal to
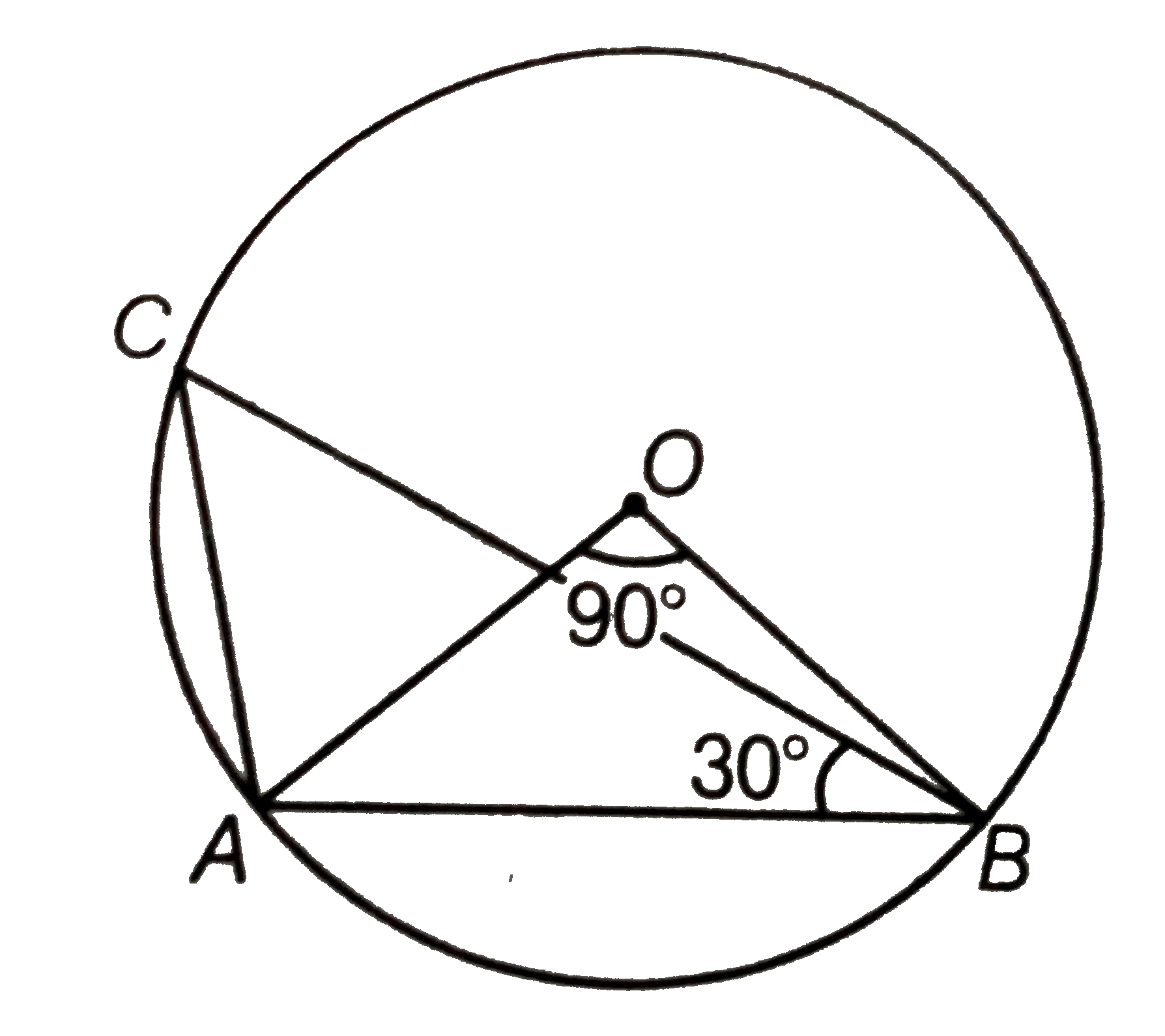 A30∘B45∘C90∘D60∘
A30∘B45∘C90∘D60∘
In the given figure, AB = BC, ∠BAC=70∘ and BC is produced to E, AC = CD and ∠ADE is the exterior angle of ΔADC. Find the angle of ∠ADE.

View SolutionIn the given figure , ∠DBC=65∘,∠BAC=35∘ and AB=BC, then the measure of ∠ECD is equal to:
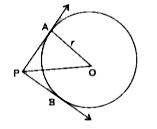
View SolutionIn the figure, ∠APB=90∘. Find the length of OP.
View SolutionIn the adjoining figure ∠BAC=60∘andBC=a,AC=bandAB=c, then :

View SolutionIn the given figure ∠BAC=79∘, CA=CB and BD=CD.Find the measurees of ∠x,∠yand∠z.

View Solution