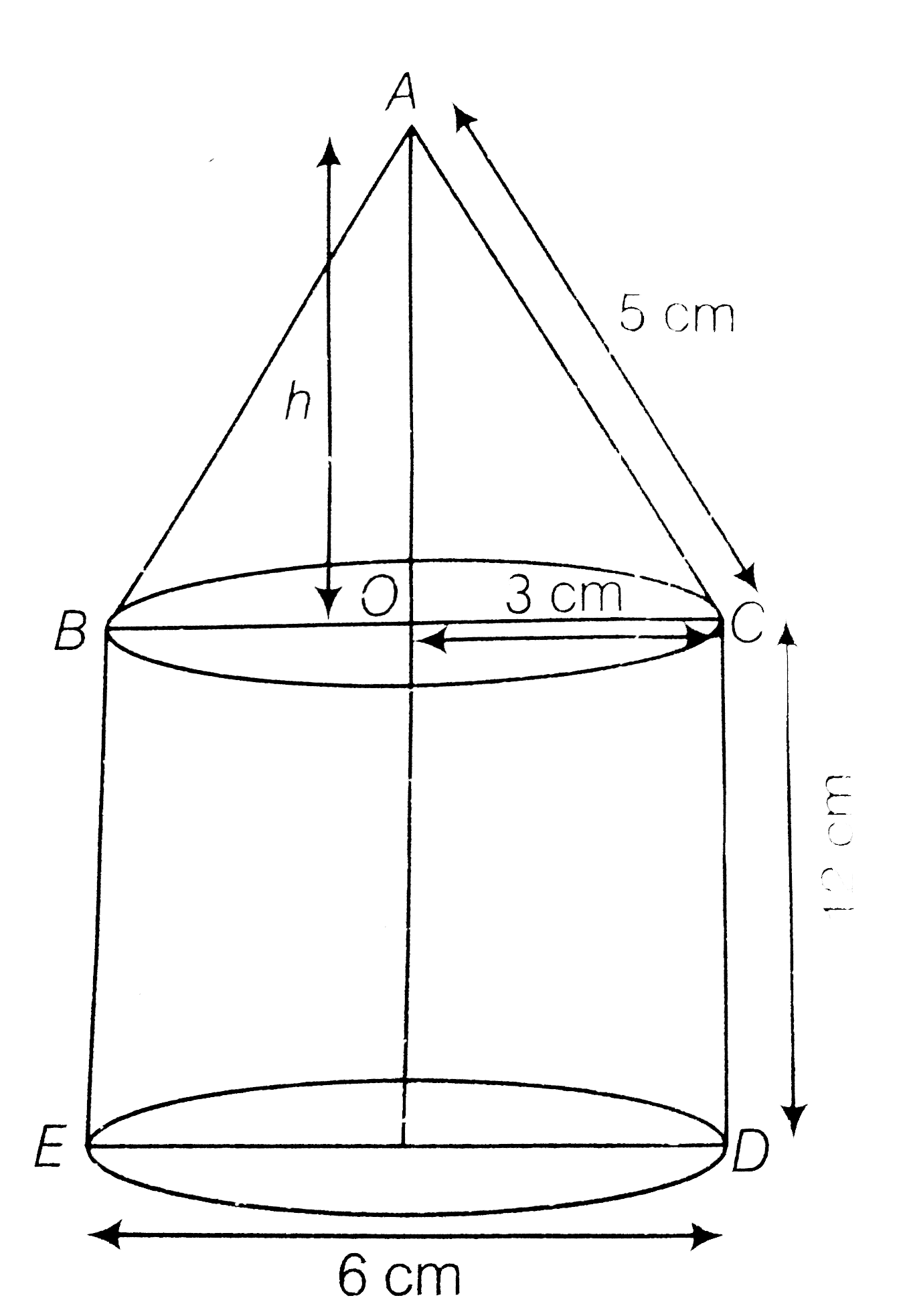
A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diamter and height of the cylinder are 6 cm and 12 cm , respectively. If the slant height of the conical portion is 5 cm, the find the total surface area and volume of the rocket. ( use $π = 3.14$ ).

Video Solution

Text Solution

Verified by Experts

Since, rocket is the combination of a right circular cylinder and a cone.
Given, diameter of the cylinder = 6 cm
$∴$ Radius of the cylinder = 12 cm
and height of the cylinder $= π r^{2} h = 3.14 \times {(3)}^{3} \times 12$
$= 339.12 c m^{3}$
and height of the cylinder = 12 cm
$∴$ Volume of the cylinder $= π r^{2} h = 3.14 \times {(3)}^{3} \times 12$
$= 339.12 c m^{3}$
and curved surface area $= 2 π r h$
$= 2 \times 3.14 \times 3 \times 12 = 226.08$
Now, in right angled $Δ A O c$
$h = \sqrt{5^{2} - 3^{2}} = \sqrt{25 - 9} = \sqrt{16} = 4$
$∴$ Height of the cone h = 4 cm
Radius of the cone ,r= 3cm
Now, volume of the cone
$= \frac{1}{3} π r^{2} h = \frac{1}{3} \times 3.14 \times {(3)}^{2} \times 4$
$= \frac{113.04}{3} = 37.68 c m^{3}$
and curved surface area $= π r l = 3.14 \times 3 \times 5 = 47.1$
Hence, total volume of the rocket $= 339.12 + 37.68 = 376.8 c m^{3}$
and total surface area of the rocket = CSA of cone + CSA of cylinder + Area of base of cylinder
$= 47.1 + 226.08 + 28.26$
$= 301.44 c m^{2}$

Updated on:21/07/2023

The volume of a right circular cylinder, 14 cm in height is equal to that of a cube whose edge is 11 cm. The radius of the base of the cylinder is (a) 5.2 cm (b) 5.5 cm (c) 11 cm (d) 22 cm
A $5.2$ cm
B $5.5$ cm
C11 cm
D22 cm
The area of the curved surface and the area of the base of a right circular cylinder are a sq cm and b gq cm respectively. The height of the cylinder is
A $\frac{22 a}{\sqrt{π b}}$ cm
B $\frac{8 \sqrt{b}}{2 \sqrt{π}}$ cm
C $\frac{a}{2 \sqrt{π b}}$ cm
D $\frac{a \sqrt{π}}{2 \sqrt{b}}$ cm
A cone was melted and cast into a cylinder of the same radius as that of the base of the cone. If the height of the cylinder is 5 cm, then what is the height of the cone?
A15 cm
B10 cm
C18 cm
D5 cm