The linear mass density of a rod of length 2L varies with distance (x) from center as λ=λ0(1+xL) .The distance of COM from center is nL.Then n is
Step by step video & image solution for The linear mass density of a rod of length 2L varies with distance (x) from center as lambda=lambda_(0)(1+(x)/(L)) .The distance of COM from center is nL.Then n is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
If linear charge density of a wire of length L depends on distance x from one end as λ=λ0(x)L .Find total charge of wire :-
View SolutionThe linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
View Solution
Knowledge Check
- Question 1 - Select One
the linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
Aλ0l33Bλ0l34C2λ0l33Dλ0l32 - Question 2 - Select One
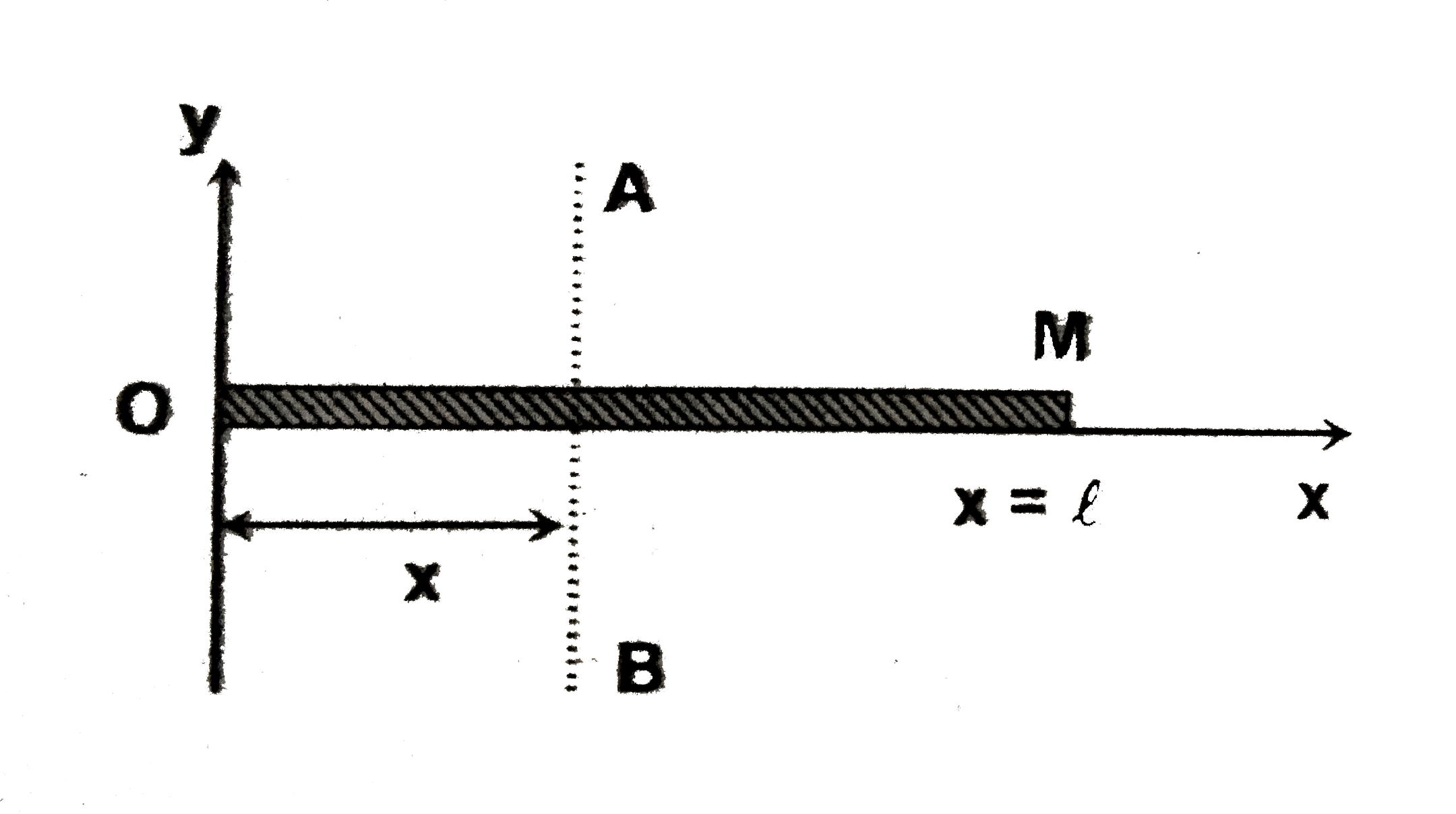
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass densty that varies with the distance x from left end of the rod according to λ=λ0(x3L3)
Where unit of λ0 is kg/m. What is the value of x so that moment of inertia of rod about axis AB (IAB) is minimum?A7l15B2l5C8l15D4l5
Linear mass density of a rod AB ( of length 10 m) varied with distance x from its end A as λ=λ0x3 (λ0 is positive constant). Distance of centre of mass the rod, form end B is
View SolutionThe density of a thin rod of length l varies with the distance x from one end as ρ=ρ0x2l2. Find the position of centre of mass of rod.
View Solution[" A wire of length "L" is placed along "x" &axis "],[" with one end at the origin.The linear charge "],[" density of the wire varies with "],[" Q."" distance "x" from the origin as "lambda=lambda_(0)((x^(3))/(L))" ."],[" Where "varnothing_(0)" is a positive constant.The total "],[" charge "Q" on the rod is "]
View SolutionLinear mass density of a rod PQ of length l and mass m is varying with the distance x (from P), as λ=m2l(1+ax)

(i) Determine the value of a
(ii) Also determine the distance of c.m. from the end P.View SolutionIf the linear density of a rod of length L varies as λ=A+Bx , find the position of its centre of mass .
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. Here, a and b are constants. Find the position of centre of mass of this rod.
View Solution
