Let ABC be an acute scalene triangle, and O and H be its circumcentre and orthocentre respectively. Further let N be the midpoint of OH. The value of the vector sum −−→NA+−−→NB+−−→NC is
→O(zero vector)
−−→HO
12−−→HO
12−−→OH
The correct Answer is:C
Circumcenter (origin O )
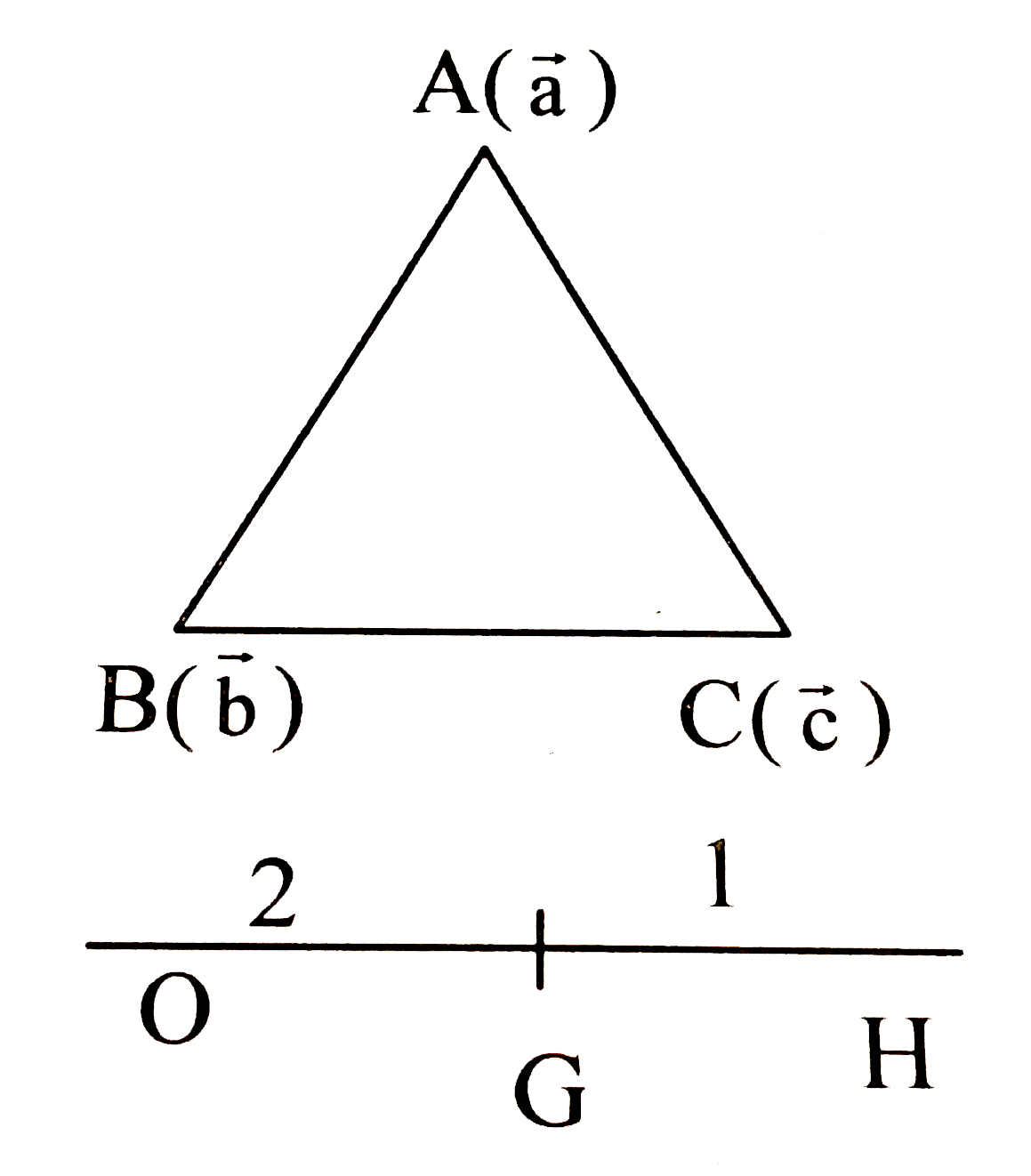
(→O)=(→a+→b+→c3),H=(→a+→b+→c2)
→N=14(→a+→b+→c)
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-1 MATHEMATICS
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHMATICS
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part A - Mathematics
20 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Let O, O' and G be the circumcentre, orthocentre and centroid of a ΔABC and S be any point in the plane of the triangle.
Statement -1: −−−→O'A+−−−→O'B+−−−→O'C=2−−−→O'O
Statement -2: −→SA+−−→SB+−−→SC=3−−→SG
View SolutionIf O is the circumcentre, G is the centroid and O' is orthocentre or triangle ABC then prove that: −−→OA+−−→OB+−−→OC=−−−→OO'
View Solution
Knowledge Check
Let H be the orthocenter of an acute - angled triangle ABC and O be itscircumcenter. Then −−→HA+−−→HB+−−→HC
Ais equal to −−→HOBis equal to −−−→3HOCis equal to −−−→2HODis not a scalar multiple of −−→HO in generalLet O, O' and G be the circumcentre, orthocentre and centroid of a ΔABC and S be any point in the plane of the triangle.
Statement -1: −−−→O'A+−−−→O'B+−−−→O'C=2−−−→O'O
Statement -2: −→SA+−−→SB+−−→SC=3−−→SGAStatement - 1 is True, Statement - 2 is True , Statement - 2 is a correct explanation for Statement - 1.BStatement -1 is True, Statement - 2 is True, Statement -2 is not a correct explanation for Statement - 1.CStatement - 1 is True, Statement - 2 is False.DStatement - 1 is False, Statement - 2 is True.Let the position vectors of the points A, B and C be →a,→band→c respectively. Let Q be the point of intersection of the medians of the triangle ABC. Then −−→QA+−−→QB+−−→QC=
A→a+→b+→c2B2→a+→b+→cC→a+→b+→cD→0
If O is the circumcentre and P the orthocentre of ΔABC, prove that −−→OA+−−→OB+−−→OC=−−→OP.
View SolutionIf O is the circumcentre, G is the centroid and O' is orthocentre or triangle ABC then prove that: −−→OA+−−→OB+−−→OC=−−−→OO'
View SolutionLet ABC be a triangle having its centroid its centroid at G. If S is any point in the plane of the triangle, then −→SA+−−→SB+−−→SC=
View SolutionLet ABC be a triangle having its centroid its centroid at G. If S is any point in the plane of the triangle, then −→SA+−−→SB+−−→SC=
View SolutionLet ABC be a triangle having its centroid its centroid at G. If S is any point in the plane of the triangle, then −→SA+−−→SB+−−→SC=
View Solution
