Let R be the set of real number and f:R→R be given by f(x)=√|x|−log(1+|x|). We now make the following assertions :
I. There exists a real number A such that f(x)≤A for all x.
II. There exists a real number B such that f(x)≥B for all x.
A
I is true and II is false
B
I is false and II is true
C
I and II both are true
D
I and II both are false
Text Solution
The correct Answer is:B
graph of given function actually look like this
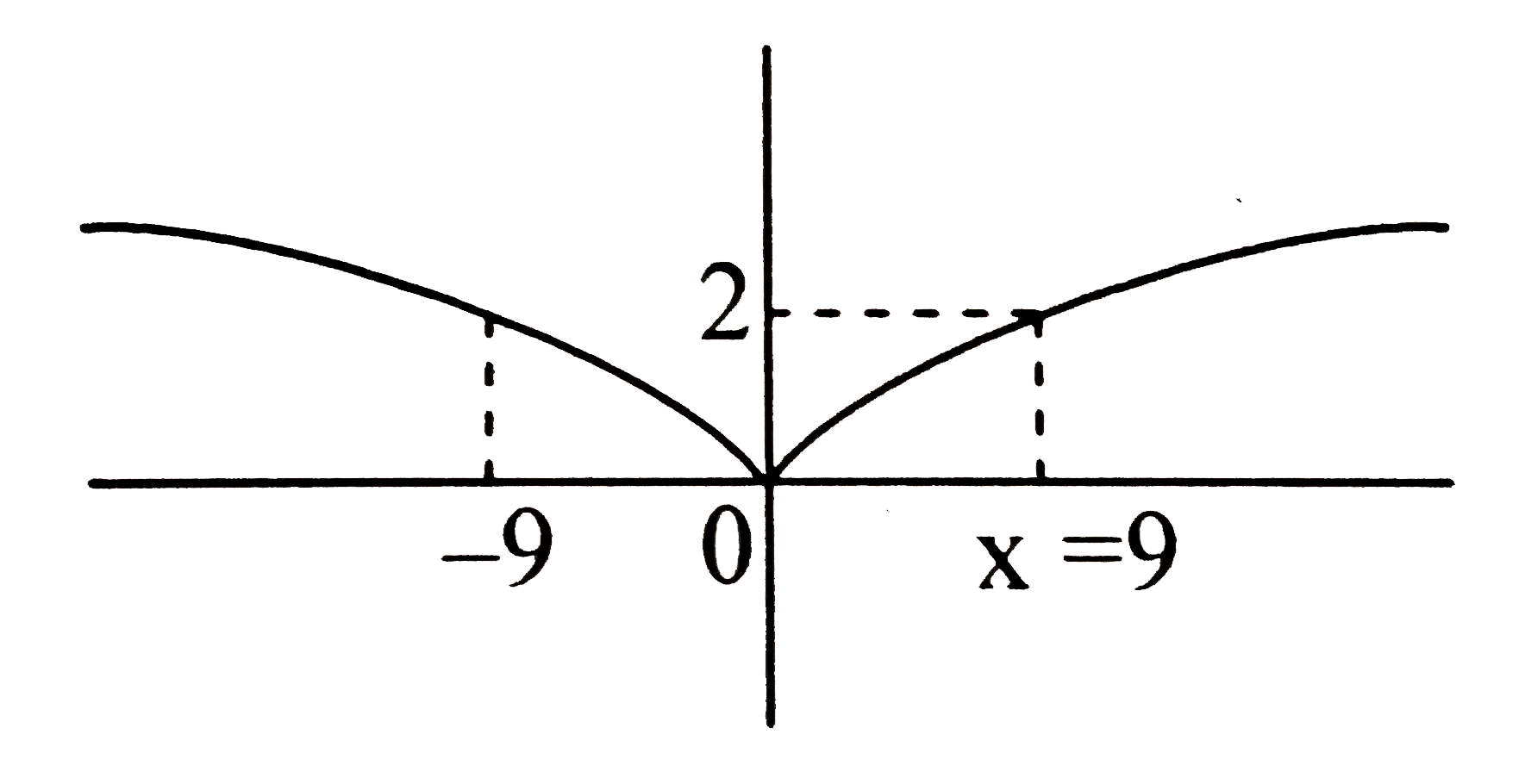
Clear from graph option (B) is right.
|
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-1 MATHEMATICS
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHMATICS
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part A - Mathematics
20 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Knowledge Check
Let R be the set of all real numbers and f : R→ R be given by f(x) = 3x2+1. Then the set f−1 ([1, 6]) is
A{−√53,0√53}B[−√53,√53]C{−√13,√13}D(−√53,√53)Let R be the set of real numbers and let f:R→R be a function such that f(x)=x21+x2. What is the range of f?
ARBR−{1}C[0,1]D[0,1)Let R be the set of all real number and f:[−1,1]→R is difined by
f(x)={xsin1x,x≠00,x=0. ThenAf satisfgies the conditions of Rolle's theorem on [−1,1]Bf satifsies the conditions of Lagrange's Mean Value Theorem on [−1,1]Cf satisfies the conditions of Rolle's theorem on [0,1]Df satisfies the conditions of Lagrange's Mean Value Theorem on [0,]
Let R be the set of real numbers and f:R→R suchthat for all x and y in R.
|f(x)−f(y)|≤|x−y|3, then f(x) is a constant.
View SolutionLet R be the set of real numbers and f:R→R be such that for all x and y in R, f(x)−f(y)∣2≤(x−y)3. Prove that f(x) is a constant.
View SolutionLet R be the set of real numbers and f:R→R be such that for all x and y in R, |f(x)−f(y)|2≤(x−y)3. Prove that f(x) is a constant.
View SolutionLet R be the set of real numbers. Define a real function f:R→R by f(x)=x+10. Sketch the graph of this function.
View SolutionLet f(x) be periodic and k be a positive real number such that f(x+k)+f(x)=0 for all x∈R. Then the period of f(x) is
View Solution
