Let a, b, c be the side-lengths of a triangle, and l, m,n be the lengths of its medians. Put K=(l+m+na+b+c) Then, as a, b, c vary, K can assume every value in the interval
(14,45)
(12,45)
(34,1)
(45,54)
The correct Answer is:C
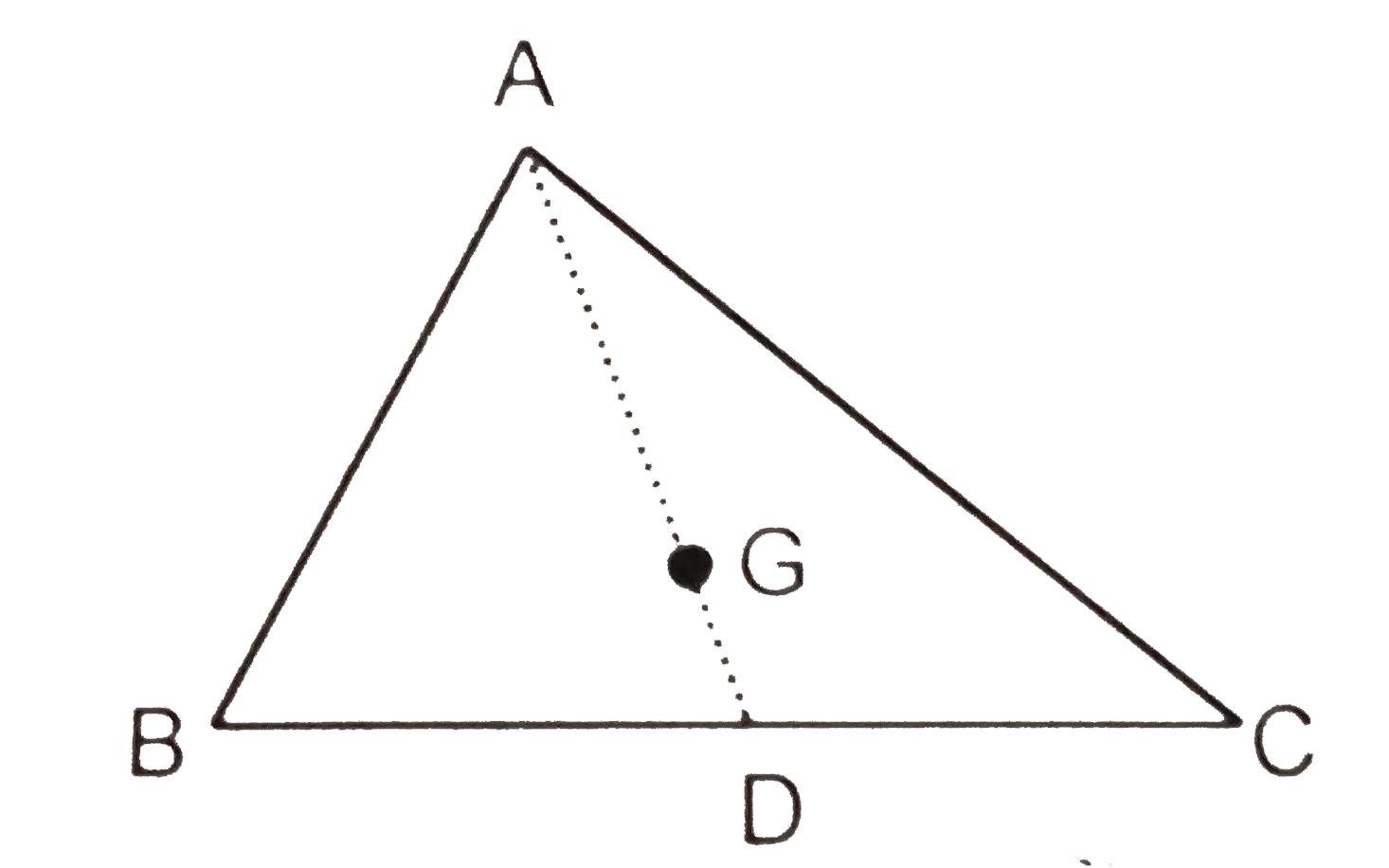
As Ad is medium ⇒AD<AB+AC2
⇒l<b+c2
Similarly m<c+a2 and n<a+b2
⇒l+m+n<a+b+c
⇒l+m+n<a+b+c
⇒l+m+na+b+c<1 (i)
Also in the ΔBGC
BG+GC>BC
⇒23(m+n)>a
Similarly 23(n+l)>b
and 23(l+m)>c
Hence 43(l+m+n)>a+b+c
l+m+na+b+c>34 (ii)
By (i) and (ii) l+m+na+b+c∈(34,1)
Topper's Solved these Questions
Similar Questions
Let a = BC, b = CA, c = AB be side lengths of a triangle ABC. And m be the length of the median through A. If a = 8, b-c = 2, m = 6, then the nearest integer to b is
View SolutionIn a triangle ABC, a, b and c are the lengths of the sides and p, q and r are the lengths of its medians.
Which one of the following is correct ?View Solution
Knowledge Check
- Question 1 - Select One or More
If a, b,c are the lengths of the sides of triangle , then
Aa−b>cBa+b<cCc=a+bDc<a+b - Question 2 - Select One or More
Let a,b,c be the sides of a triangle ABC, a=2c,cos(A-C)+cos B=1. then the value of C is
Aπ/6Bπ/3C2π/3D5π/6 - Question 3 - Select One
Let a = BC, b = CA, c = AB be side lengths of a triangle ABC. And m be the length of the median through A. If a = 8, b-c = 2, m = 6, then the nearest integer to b is
A7B8C9D10
Let a, b, c be the lengths of the sides of a triangle (no two of them are equal) and k∈R.If the roots of the equation x2+2(a+b+c)x+6k(ab+bc+ac)=0 are real, then:
View SolutionIf a, b and c represent the lengths of sides of a triangle then the possible integeral value of ab+c+bc+a+ca+b is _____
View SolutionLet a≤b≤c be the lengths of the sides of a triangle. If a2+b2<c2, then prove that triangle is obtuse angled .
View SolutionLet ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. The maximum value of the product (lalblc)×cos2(B−C2)×cos2(C−A)2)×cos2(A−B2) is equal to :View SolutionLet ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. The maximum value of the product (lalblc)×cos2(B−C2)×cos2(C−A)2)×cos2(A−B2) is equal to :View Solution

