Let PQR be a triangle which PQ = 3. Form the vertex R, draw the altitude RS to meet PQ at S. Assume that RS=√3 and Ps=QR. Then PR equals
A
√5
B
√6
C
√7
D
√8
Video Solution
Text Solution
The correct Answer is:C

PS=QR
PS+SQ=3
in De<RSQ Sq=3−PS=3−QR
QR2=RS2+SQ2
QR2=3+(3−QR)2
QR2=3+9+QR2−6QR
6QR=12
QR=2
SQ=1 PS=2
in ΔRSP
PR2=RS2+PS2
=3+4
PR2=7
PR=√7
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Let PQR be am acute-angled triangle in which PQ lt QR. From the vertex Q draw altitude Q1, the angle bisector QQ2 and the medianQQ3 With Q1,Q2,Q3 lying on PR. Then
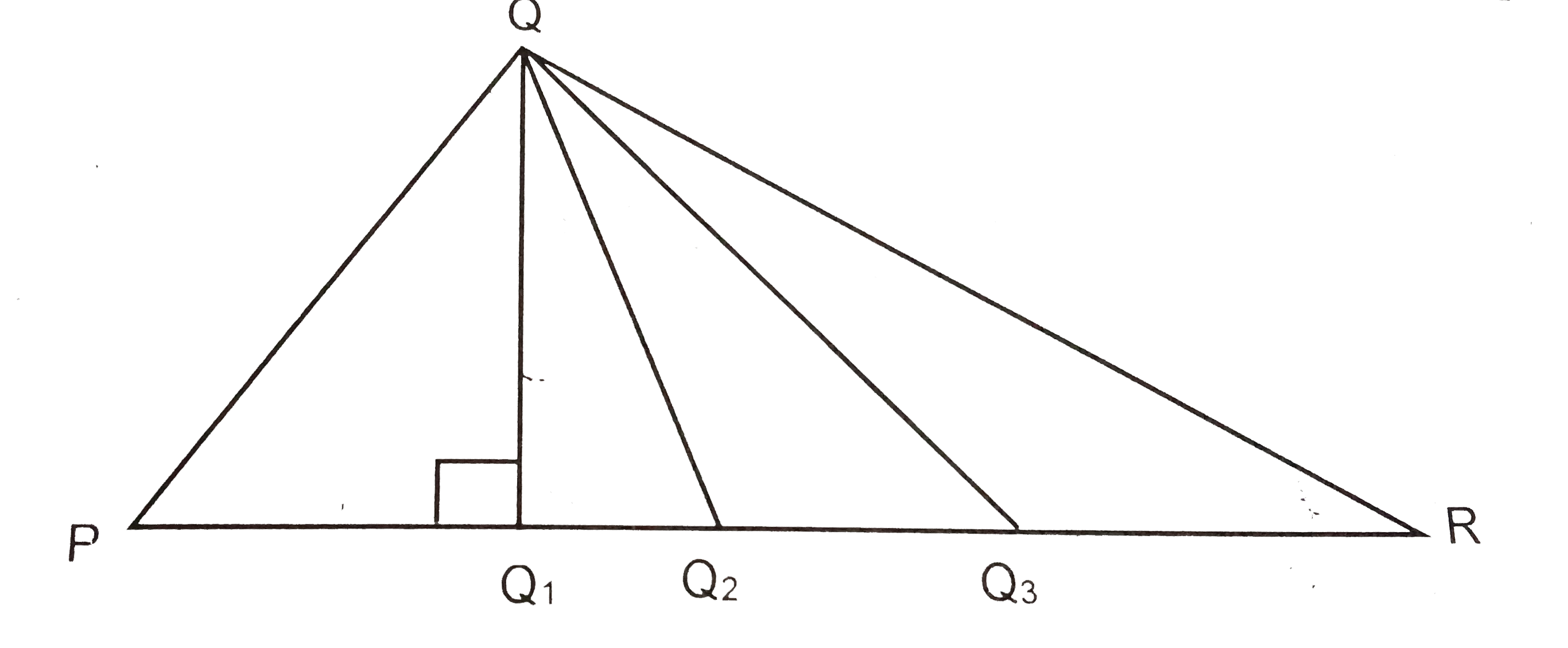 APQ1<PQ2<PQ3BPQ2<PQ1<PQ3CPQ1<PQ3<PQ2DPQ3<PQ1<PQ2
APQ1<PQ2<PQ3BPQ2<PQ1<PQ3CPQ1<PQ3<PQ2DPQ3<PQ1<PQ2 - Question 2 - Select One
In a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of these - Question 3 - Select One
In a triangle PQR, PQ=20 cm and PR =6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of the above
Construct a triangle PQR in which QR = 6cm, ∠Q=60∘ and PR – PQ = 2cm.
View SolutionPQR is a triangle is which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT
In△PQR,wehavePQ=PRView SolutionPQRis a triangle such that PQ=PR.RSand QT are the medians to the sides PQandPR respectively. If the medians RS and GT intersect at right angle, then what is the value of (PQQR)2 ?
View SolutionLet □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
View SolutionPQR is a triangle in which PR=QR. Side PR is extended to S, such that QR=RS. If ∠QPR=40∘, then what is the value (in degrees) of ∠QSR?
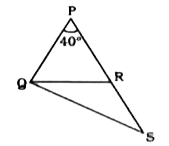 View Solution
View Solution

