Let $O P = r and ∠ X O P = θ$ then the position of P in polar coordinate system is represented by $(r, θ)$ OX and O are called the initial line and pole respectively.
If p be the length of perpendicular from origin to line and if $α$ is the angle which the perpendicular to the line makes with the initial line . The equation of line is given by r cos $(θ - α) = p$

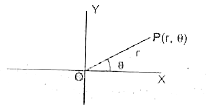
The equation of straight line $x + \sqrt{3} y = 1$ in polar coordinate is

$r = \frac{1}{2} cos (θ + \frac{π}{6})$

$2 r - cosec (θ + \frac{π}{6})$

$r = sin (θ + \frac{π}{6})$

$r = 2 cos (θ + \frac{π}{6})$

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINE

Topper's Solved these Questions

Knowledge Check

Let $O P = r and ∠ X O P = θ$ then the position of P in polar coordinate system is represented by $(r, θ)$ OX and O are called the initial line and pole respectively.
If p be the length of perpendicular from origin to line and if $α$ is the angle which the perpendicular to the line makes with the initial line . The equation of line is given by r $cos (θ - α) = p$

The polar coordinates of the foot of perpendicular from the pole on the line joining the two points $(r_{1}, θ_{1}) and (r_{2}, θ_{2})$ are
A $⎡ ⎢ ⎢ ⎣ \frac{r_{1} r_{2} sin (θ_{2} - θ_{1})}{\sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} cos (θ_{1} - θ_{2})}}, {tan}^{- 1} (\frac{r_{1} {cos θ}_{1} - r_{2} {cos θ}_{2}}{r_{2} {sin θ}_{2} - r_{1} {sin θ}_{2}}) ⎤ ⎥ ⎥ ⎦$
B $⎡ ⎢ ⎢ ⎣ \frac{r_{1} r_{2} sin (θ_{2} + θ_{1})}{\sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} cos (θ_{1} - θ_{2})}}, {tan}^{- 1} (\frac{r_{1} {cos θ}_{1} - r_{2} {cos θ}_{2}}{r_{2} {sin θ}_{2} - r_{1} {sin θ}_{1}}) ⎤ ⎥ ⎥ ⎦$
C $⎡ ⎢ ⎢ ⎣ \frac{- r_{1} r_{2} sin (θ_{2} - θ_{1})}{\sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} cos (θ_{1} - θ_{2})}}, {tan}^{- 1} (\frac{r_{1} {cos θ}_{1} - r_{2} {cos θ}_{2}}{r_{2} {sin θ}_{2} - r_{1} {sin θ}_{1}}) ⎤ ⎥ ⎥ ⎦$
Dnone of these
Let $O P = r and ∠ X O P = θ$ then the position of P in polar coordinate system is represented by $(r, θ)$ OX and O are called the initial line and pole respectively.
If p be the length of perpendicular from origin to line and if $α$ is the angle which the perpendicular to the line makes with the initial line . The equation of line is given by r cos $(θ - α) = p$

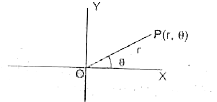
Perpendicular distance from pole to the line $\frac{l}{r} = 4 cos θ + 2 sin θ$ is
A $2 \sqrt{5}$
B $\frac{l}{2 \sqrt{5}}$
C $\frac{2 \sqrt{5}}{l}$
Dnone of these
The length of perpendicular from the origin to a line is 5 units and the line makes an angle $120^{\circ}$ with the positive direction of x-axis. The equation of the line is
A $x + \sqrt{3} y = 5$
B $\sqrt{3} x + y = 10$
C $\sqrt{3} x - y = 10$
DNone of these

FIITJEE-STRAIGHT LINE -COMPREHENSIONS

Home
Ask Doubt
Profile

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

The length of perpendicular from the origin to a line is 5 units and the line makes an angle 120∘ with the positive direction of x-axis. The equation of the line is

FIITJEE-STRAIGHT LINE -COMPREHENSIONS

The length of perpendicular from the origin to a line is 5 units and the line makes an angle $120^{\circ}$ with the positive direction of x-axis. The equation of the line is