A small uncharged metallic sphere is positioned exactly at a point midway between two equal and opposite point charges. If the sphere is slightly displaced towards the positive charge and released, then
it will oscillate about its original position
it will move further towards the positive charge
its potential energy will decrease and kinetic energy will increase
the total energy remains constant but is non-zero
The correct Answer is:B, C, D
To solve the problem step by step, we will analyze the situation involving the small uncharged metallic sphere placed between two equal and opposite point charges.
Step 1: Understanding the Initial Setup
We have two point charges:
- Charge +q (positive charge)
- Charge −q (negative charge)
These charges are positioned at equal distances from a small uncharged metallic sphere, which is placed at the midpoint between them.
Step 2: Polarization of the Sphere
When the uncharged metallic sphere is placed in the electric field created by the two point charges, it becomes polarized. This means that:
- The side of the sphere closer to the positive charge will have a slight negative charge induced on it (due to the attraction of electrons).
- The side of the sphere closer to the negative charge will have a slight positive charge induced on it (due to the repulsion of electrons).
Step 3: Displacement of the Sphere
Now, if we slightly displace the sphere towards the positive charge and release it, we need to analyze the forces acting on it:
- The force due to the positive charge (F1) will attract the induced negative charge on the sphere.
- The force due to the negative charge (F2) will repel the induced positive charge on the sphere.
Step 4: Analyzing the Forces
When the sphere is displaced towards the positive charge:
- The distance from the positive charge becomes r−x (where x is the displacement).
- The distance from the negative charge becomes r+x.
The magnitudes of the forces can be expressed as:
- F1=k⋅q⋅(−qinduced)(r−x)2
- F2=k⋅q⋅(+qinduced)(r+x)2
Since (r−x)<(r+x), it follows that F1>F2. Therefore, the net force acting on the sphere will be directed towards the positive charge.
Step 5: Motion of the Sphere
As a result of the net force being directed towards the positive charge:
- The sphere will accelerate towards the positive charge.
- It will not oscillate around the midpoint but will continue to move towards the positive charge.
Step 6: Energy Considerations
As the sphere moves:
- Its potential energy decreases because it is moving in the direction of the electric field created by the positive charge.
- Its kinetic energy increases as it accelerates towards the positive charge.
Conclusion
Thus, the correct interpretation of the situation is:
- The sphere will not oscillate about its original position; instead, it will move towards the positive charge.
- The potential energy of the sphere will decrease while its kinetic energy will increase.
Final Answer
The correct option is that the sphere will move towards the positive charge and will not oscillate.
---
We have two point charges:
- Charge +q (positive charge)
- Charge −q (negative charge)
When the uncharged metallic sphere is placed in the electric field created by the two point charges, it becomes polarized. This means that:
- The side of the sphere closer to the positive charge will have a slight negative charge induced on it (due to the attraction of electrons).
- The side of the sphere closer to the negative charge will have a slight positive charge induced on it (due to the repulsion of electrons).
Now, if we slightly displace the sphere towards the positive charge and release it, we need to analyze the forces acting on it:
- The force due to the positive charge (F1) will attract the induced negative charge on the sphere.
- The force due to the negative charge (F2) will repel the induced positive charge on the sphere.
When the sphere is displaced towards the positive charge:
- The distance from the positive charge becomes r−x (where x is the displacement).
- The distance from the negative charge becomes r+x.
- F1=k⋅q⋅(−qinduced)(r−x)2
- F2=k⋅q⋅(+qinduced)(r+x)2
As a result of the net force being directed towards the positive charge:
- The sphere will accelerate towards the positive charge.
- It will not oscillate around the midpoint but will continue to move towards the positive charge.
As the sphere moves:
- Its potential energy decreases because it is moving in the direction of the electric field created by the positive charge.
- Its kinetic energy increases as it accelerates towards the positive charge.
Thus, the correct interpretation of the situation is:
- The sphere will not oscillate about its original position; instead, it will move towards the positive charge.
- The potential energy of the sphere will decrease while its kinetic energy will increase.
The correct option is that the sphere will move towards the positive charge and will not oscillate.
Topper's Solved these Questions
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - COMPREHENSION BASED (COMPREHENSION - II)
3 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - (PROBLEM SOLUTION) COMPREHENSION - I (COMPREHENSION BASED TYPE)
3 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL - I
24 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
21 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
Similar Questions
How can you charge a metal sphere positively without touching it?
View SolutionA small uncharged sphere is positioned exactly in the midpoint between two charges whose absolute values are the same but whose signs are opposite. Suppose the sphere is shifted sornewhat. Will it remain in the new position or will it move in some direction?
View Solution
Knowledge Check
An uncharged metal sphere is placed between two equal and oppositely charged metal plates. The nature of lines of force will be
A B
B C
C D
D
Consider a neutral conducting sphere. A positive point charge is placed outside the sphere. The net charge on the sphere is then
ANegative and uniformly distributed over the surface of sphereBPositive and uniformly distributed over the surface of sphereCNegative and appears at a point the surface of sphere closest to point chargeDZeroTwo identical metallic spheres A and B of exactly equal masses are given equal positive and negative charges respectively. Then
Amass of A > mass of BBmass of A < Mass of BCmass of A= Mass of BDmass of A ≤ Mass of B
A. small uncharged metal sphere is suspended hy a long nonconducting string in the region between the vertically positioned plates of a parallel-plate capacitor, closer to one plate than to the other. How will the sphere behave?
View SolutionA metallic sphere is kept in between two oppositely charged plates. The most appropriate representation of the field lines is -
View SolutionA sphere is constructed around a positive point charge q. The work done in moving a unit positive charge on this sphere is numerically equal to
View SolutionA positive point charge q is brought near a neutral metal sphere.
View SolutionTwo uncharged metal spheres, L and M, are in contact A positively charged rod is brought close to L, but not touching it, as shown. The two spheres are slightly separated and the rod is then withdrawn. As a result:
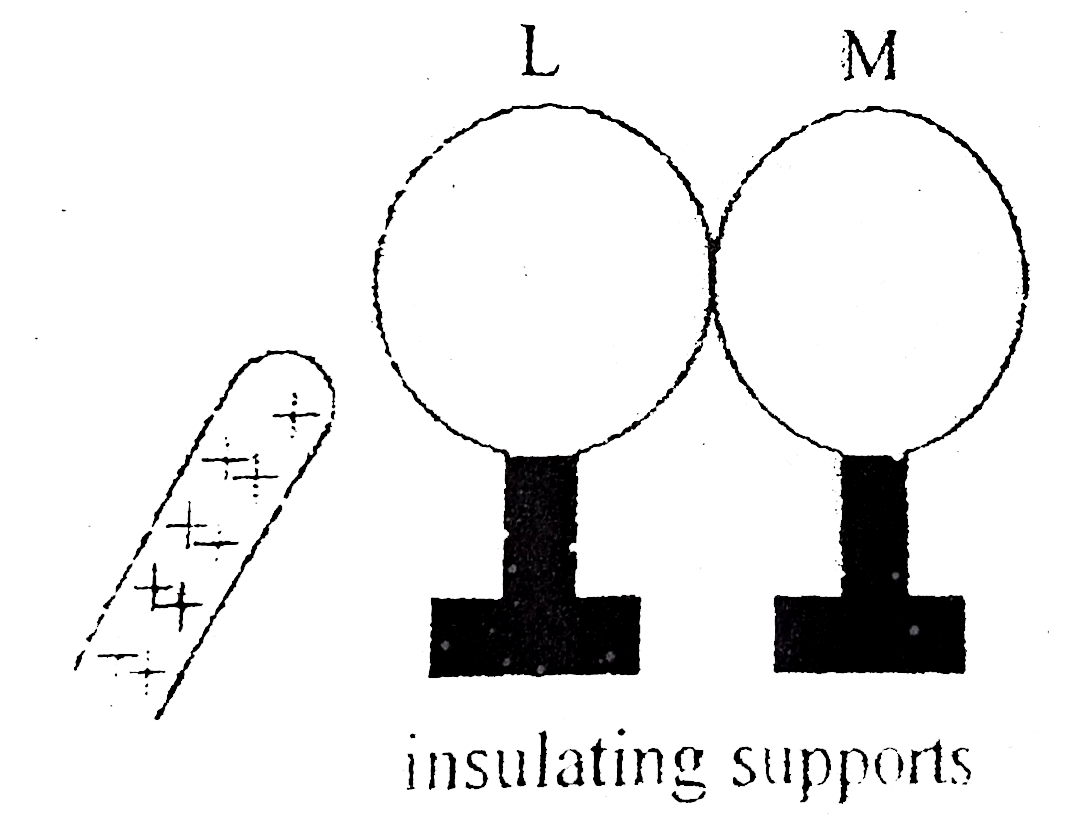
View Solution
