Given a fixed circle C and a line L through the centre O of C. Take a variable point P and L and let K be the circle centre P through O. Let T be the point weere a common tangent to C and K meets K. The locus of T is

a circle

a parabola

a pair of straight lines

none of these

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A tangent AB at a point A of a circle of radius 5 cm meets a line through the centre O at a point B so that OB = 12 cm , Length AB is
A10 cm
B12 cm
C9 cm
D $\sqrt{119}$ cm
TP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ?

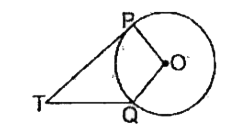ANo
BYes
CCannot say
DData insufficient
ABCD is a square of side length 2. $C_{1}$ is a circle inscribed in the square and $C_{2}$ is a circle. circumscribing the square. P and Q are any two points on $C_{1} and C_{2}$ respectively. Also R is fixed point and L is a fixed line in the same plane. A circle C touches line L and circle $C_{1}$ externally. S is a point which is equidistant from given point Rand fixed line L. Point R coincides with B.
Let L be the line joining any two adjacent points of the square. The locus of centre of this circle C is :
Aparabola
Bellipse
Cpair of straight lines
Dhyperbola