TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
To prove that line segment AP bisects the angle TAB, we will follow these steps:
Step 1: Identify the Given Elements
We have a circle with center O and an external point T from which two tangents TA and TB are drawn to the circle. The line OT intersects the circle at point P.
Step 2: Draw the Diagram
Draw the circle with center O, the external point T, and the tangents TA and TB. Mark the intersection point P where OT intersects the circle.
Step 3: Establish Triangle Congruence
In triangles TAP and TBP:
- TA = TB (since both are tangents from point T to the circle)
- Angle ATP = Angle BTP (because OT is a transversal line intersecting the tangents TA and TB)
- TP = TP (common side)
Step 4: Apply the SAS Congruence Criterion
Since we have:
- TA = TB
- Angle ATP = Angle BTP
- TP = TP
By the Side-Angle-Side (SAS) congruence criterion, we can conclude that triangle TAP is congruent to triangle TBP.
Step 5: Conclude Corresponding Angles
From the congruence of triangles TAP and TBP, we know that:
- Angle TAP = Angle TBP (corresponding parts of congruent triangles are equal)
Step 6: Use Alternate Segment Theorem
According to the alternate segment theorem, we have:
- Angle TBP = Angle BAP (angles in the alternate segments are equal)
Step 7: Relate the Angles
From the previous steps, we can relate the angles:
- Angle TAP = Angle BAP (since Angle TAP = Angle TBP and Angle TBP = Angle BAP)
Step 8: Conclusion
Since Angle TAP = Angle BAP, we conclude that line segment AP bisects angle TAB.
Thus, we have proved that AP bisects angle TAB.
---
We have a circle with center O and an external point T from which two tangents TA and TB are drawn to the circle. The line OT intersects the circle at point P.
Draw the circle with center O, the external point T, and the tangents TA and TB. Mark the intersection point P where OT intersects the circle.
In triangles TAP and TBP:
- TA = TB (since both are tangents from point T to the circle)
- Angle ATP = Angle BTP (because OT is a transversal line intersecting the tangents TA and TB)
- TP = TP (common side)
Since we have:
- TA = TB
- Angle ATP = Angle BTP
- TP = TP
From the congruence of triangles TAP and TBP, we know that:
- Angle TAP = Angle TBP (corresponding parts of congruent triangles are equal)
According to the alternate segment theorem, we have:
- Angle TBP = Angle BAP (angles in the alternate segments are equal)
From the previous steps, we can relate the angles:
- Angle TAP = Angle BAP (since Angle TAP = Angle TBP and Angle TBP = Angle BAP)
Since Angle TAP = Angle BAP, we conclude that line segment AP bisects angle TAB.
Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
Two tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTangents AP and AQ are drawn to a circle, with centre O, from an exterior point A.
Porve that :
∠PAQ=2∠OPQ
View SolutionIn the figure, PO⊥QO. The tangents to the circle with centre O at P and Q intersect at a point T. Prove that PQ and OT are right bisectors of each other.

View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
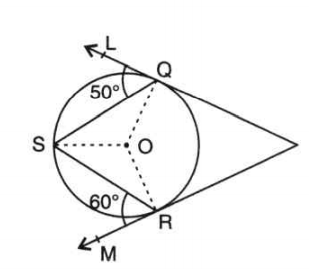
View SolutionIn the given figure, PQL and PRM are two tangents to the circle with centre O at the point Q and R respectively. If S is a point on the circle such that angle SQL = 50° and sk... o angle SRM = 60°. Find the reflex angle QOR.
View SolutionTwo tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is cyclic quadrilateral.
View SolutionIn Figure, PA and PB are tangents from an external point P to a circle with centre O . LN touches the circle at M . Prove that PL+LM=PN+MN .
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre O from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionTwo tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
View Solution
