Question

Volume of hollow cylinder

Explanation

Volume of hollow cylinder

The volume of a cylinder is the quantity of material that it can carry or how much material can be displaced when the cylinder is immersed in it. The material could be a fluid amount or any substance which can be filled in the cylinder uniformly. This has been clarified in this article quickly alongside solved examples for better understanding.

Cylinder  Definition

The cylinder is a three-dimensional figure with a circular base. A cylinder is like a big pile of same circular discs stacked together. It will help you remember the Cylinder volume formula. The volume of a cylinder is πr²h, where r is the radius of the circle on the cylinder’s end.

The cylinders are basically of two types:

• Solid Cylinder


• Hollow Cylinder

In this article, we will focus on the hollow cylinder and its volume formula.

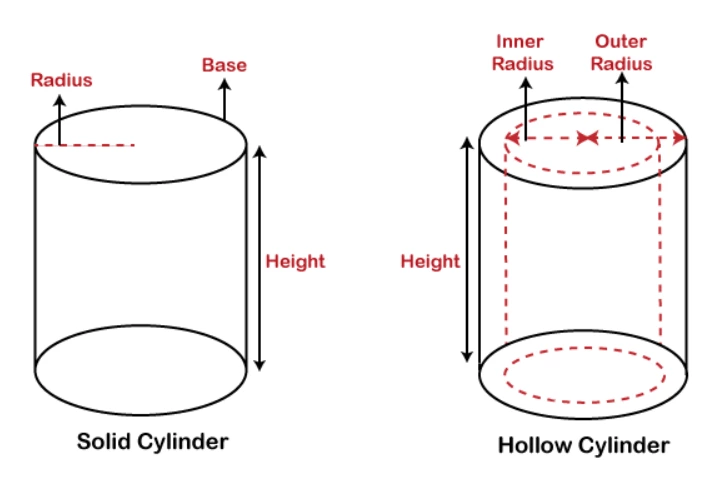
Hollow Cylinder

A hollow cylinder is one which is empty from inside and has some difference between the internal and external radius. We see hollow cylinders every day in our day to day lives. Tubes, circular buildings, straws these are all examples of a hollow cylinder.

How to find Volume of Hollow Cylinder?

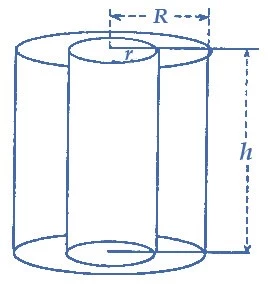
In a hollow cylinder, the circular bases have two radii, one for the inner circle and other for the outer circle. Suppose, ‘R’ and ‘r’ are the two radii of the hollow cylinder with the height of ‘h’ measure, then the volume of this cylinder can be written as;

i)         V=πR²h–πr²h=π(R²–r²)h

(ii)        V=π/4(D²–d²)

Here, d and D are the inner and the outer diameter, and V is volume.

 

Related Videos:

• Area and Perimeter of rectangle


• Area and Perimeter of square


• Area and Perimeter of triangle


• Area and Perimeter of trapezium


• Area and Perimeter of rhombus


• Area and Perimeter of circle

Solved Examples on Volume of Hollow Cylinder

Example 1:The volume of a cylindrical pipe is 1884 cu.cm. Its length is 12 cm, and its external radius is 9  cm. Find its thickness.

Solution : Here, R = external radius of the pipe = 9 cm.

h = length of the pipe = 12 cm

V = volume of the pipe = 1884 cu.cm

Let r be the internal radius.

Now, the volume of pipe = π R ² h - π r ² h

V = π ( R ² - r ² ) x h

⇒ 1884 = 3.14 ( 9 ² - r ² ) x 12

⇒ 1884 = 37.68 ( 81 - r ² )

⇒ 1884 / 37.68 = 81 - r ²

⇒ 50 = 81 - r ²

⇒ r ² = 81 – 50

⇒ r ² = 31

⇒ r = 31  cm = 5.56 cm

∴ Thickness of the pipe = R – r = 9 – 5.56 = 3.44 cm.

Example 2: A well with a 10 m inside diameter is dug 21 m deep. The mud extracted out of it is spread all around to a width of 5 m to form an embankment. Find the height of the embankment.

Solution:

The volume of the dugout well =πr²h

=22/7×5×5×21

=22 x 5 x 5 x 3

= 1650 cm³    

Area of the embankment (shaded portion)

=π(R²–r²)= π(10²–5²)           

=75×22/7 sq.m = 1650/7 sq. m.

∴ Height of the embankment

=Volume of the dugout well/Area of the embankment

=1650x 7/1650 =7 m

Height of the embankment is 7 m

Example 3 : A metal pipe is 210 cm long. Its inner and outer diameters are 6 cm and 12 cm, respectively. Find the volume of the metal used to make the pipe.

Solution:

Height of the cylindrical pipe, h=210 cm

h=210 cm

∴ External radius, R=12/2=6 cm

Internal radius, R=6/2=3cm

Volume of the metal used in making the pipe

= volume of the external cylinder – volume of the internal cylinder

=πR²h–πr²h=π(R²–r²)h=22/7[6²–3²]×210

=22×25×30=16500 cm³

 Therfore, the volume of the metal used in making the pipe is 16500 cm³

Example 4: Find the volume of a cylinder whose height is 3 m and whose base area is 250 m².

Solution

Let r and h be the radius and height of the cylinder, respectively.

Given that, height h = 3 m, base area = 250 m²

Now, the volume of a cylinder = πr²h cu. Units

= base area × h

= 250×3= 750  m³

Therefore,  the volume of the cylinder = 750  m³

Example 5: The volume of a cylindrical tank is 1.078 × 10⁶ litres. If the diameter of the tank is 8 m, calculate the height of the tank.

Solution

Suppose, r and h are the radius and height of the cylinder, respectively.

Given that, the volume of the tank = 1.078 ×10⁶ = 1078000 litre

Since 1 litre = 1/1000 m³

Therefore, Volume of the tank = 1078 m³ 

 diameter = 8m

Radius ‘r’= 8/2 m = 4m

volume of the cylindrical tank = πr²h cu. Units

1078  = 22/7 × 4 × 4 ×h

1078x7 / 22 x 16 = h

23716/352 = h

h = 67.375 m

Therefore, the height of the cylindrical tank is 67.375 m

Example 6: Find the volume of the copper used to make a pipe of height 9 cm and whose inner and outer diameters are 42 cm and 56 cm respectively.

Solution: Take,  r, R and h, as the internal radius, external radius and height of the pipe respectively.

‘d’ is the inner diameter and ‘D’ is the outer diameter

Given that, d =42cm, R = 56 cm, h = 9 cm

Let us find innner and outer radii

r= d/2 =42/2 = 21 cm

R=D/2= 56/2 = 28 cm

Now, the volume of hollow cylinder = π(R² −r² )h cubic Units

= 22/7 (28² − 21² )×9

= 22/7 (784 − 441) ×9 = 9702

Hence, the volume of copper used in making pipe = 9702 cm³

Example 7: The inner and outer radii of an iron pipe is 5 cm and 7 cm, respectively. The measure of the height of the pipe is 15 cm. Find the volume of the pipe. (π =3.14)

Solution: Let r, R and h be the internal radius, external radius and height of the pipe respectively.

Given,

radius of inner cylinder  = 6 cm

radius of inner cylinder = 8 cm

Height = 15 cm

π =22/7=3.14

Volume of the hollow cylinder (V) = π(R² −r² )h cubic Units

Substituting the values in the above formula:

The volume of iron pipe=3.14×15×(7²-5²)

V=3.14×15×(49-25)

V=3.14×15×24

V=1130.4 cm³

Important Chapters:

• NCERT Solutions for Maths


• NCERT Solution for Class 6 Maths Chapter Mensuration


• NCERT Solution for Class 8 Maths Chapter Mensuration