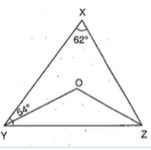
In Fig. 6.40, ∠X=62∘,∠XYZ=54∘. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.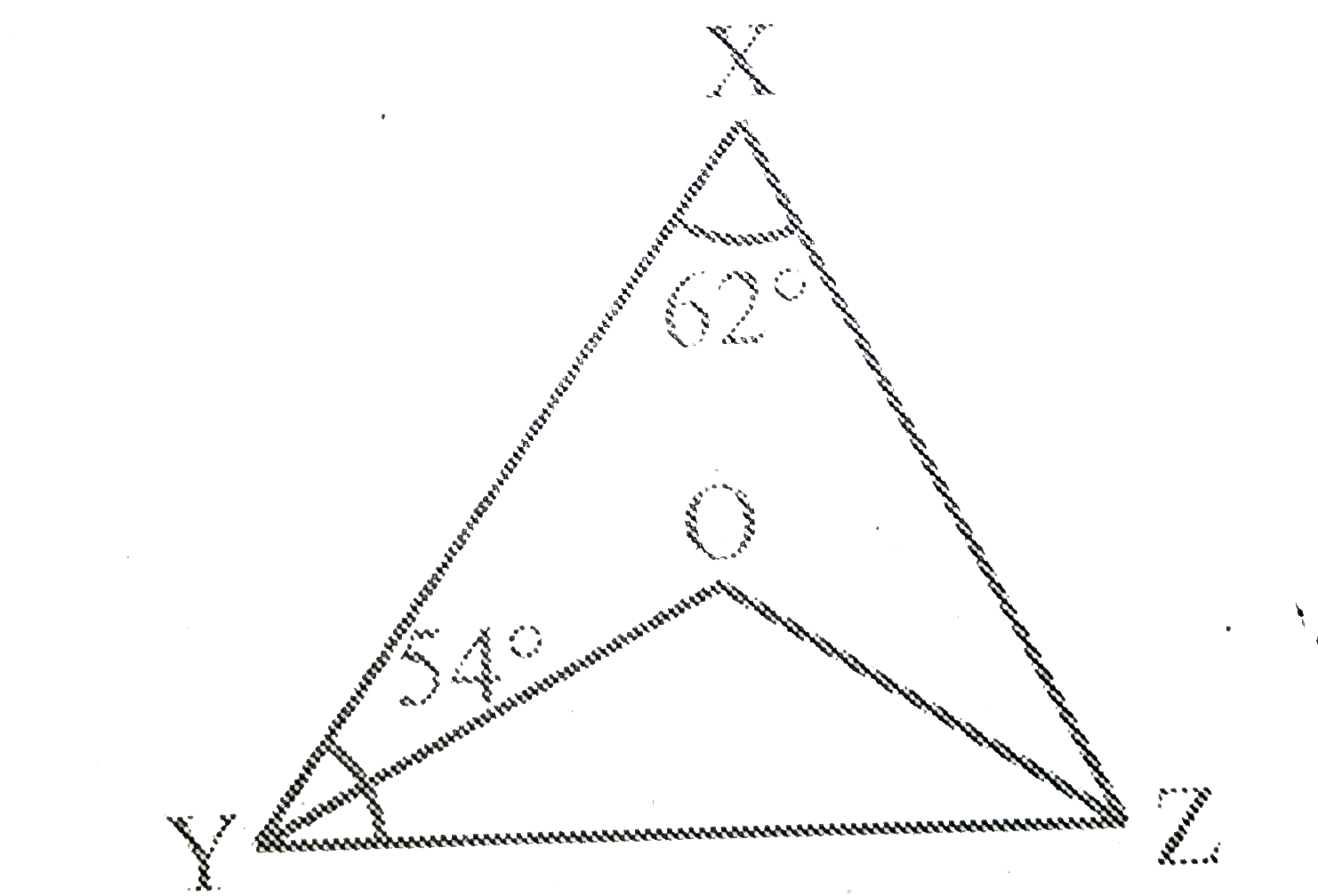
Video Solution
Text Solution
As the sum of all interior angles of a triangle is 180º, therefore, for △XYZ,
∠X+∠XYZ+∠XZY=180∘
62∘+54∘+∠XZY=180∘
∠XZY=180∘−116∘
∠XZY=64∘
∠OZY=32∘ (OZ is the angle bisector of ∠XZY)
Similarly, ∠OYZ=27∘
Using angle sum property for △OYZ, we obtain
∠OYZ+∠YOZ+∠OZY=180∘
27∘+∠YOZ+32∘=180∘
∠YOZ=180∘−59∘
∠YOZ=121∘
|
Similar Questions
Knowledge Check
If ⎡⎢⎣x−y−z−y+zz⎤⎥⎦=⎡⎢⎣053⎤⎥⎦ then the values of x,y and z are respectively
A5,2,2B1,−2,3C0,−3,3D11,8,3If x, y, z are real numbers such that x+y+z=4 and x2+y2+z2=6, then x,y,z lie in :
A[3/2,2]B[2/3,2]C[0,2/3]Dnone of theseIf x=yz,y=zx and z=xy, then
Axyz=1Bxyz=1Cx+y+z=1Dxz = y
If x(x+y+z)=4,y(x+y+z)=16andz(x+y+z)=29 and x, y & z are positive numbers. Find x, y & z=?
View SolutionIf x,zandy are in A.P. where x,y and z are distinct numbers then evaluate xx−z+zy−z
View Solutionx+y+z=6
x−y+z=2
2x+y−z=1
then x,y,z are respectively
View SolutionIf x(x+y+z)=20,y(x+y+z)=30andz(x+y+z)=50 the vaue of 2 (x + y + z) is
View SolutionIf x(x+y+z)=20,y(x+y+z)=30andz(x+y+z)=50 the vaue of 2 (x + y + z) is
View Solution