A solid in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π. Solution in Kannada
The correct Answer is:πcm3
Step by step video, text & image solution for A solid in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of pi. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - EXERCISE 15.39videos
SURFACE AREAS AND VOLUMES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - EXERCISE 15.45videos
SURFACE AREAS AND VOLUMES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - EXERCISE 15.45videos
SURFACE AREAS AND VOLUMES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - STATISTICSEXERCISE - Exercise 13.44videos
STATISTICS
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Exercise 2.6 (Optional)8videos
TRIANGLES
Similar Questions
A metallic sphere of radius 4.2cm is melted and recast into the shape of a cylinder of radius 6cm. Find the height of the cylinder.
02:00View SolutionA drinking glass is in the shape of a frustum of a cone of height 14cm . The diameters of its two circular ends. are 4cm and 2cm . Find the capacity of the glass.
01:30View SolutionA drinking glass is in the shape of a frustum of a cone of height 14cm . The diameters of its two circular ends. are 4cm and 2cm . Find the capacity of the glass.
02:36View SolutionThe following distribution gives the daily income of 50 workers of a factory.
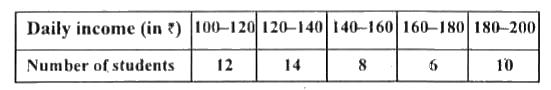
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.02:02View SolutionIn Fig . PS is the bisecto of ∠QPRofΔPQR . Prove that
QSSR=PQPR
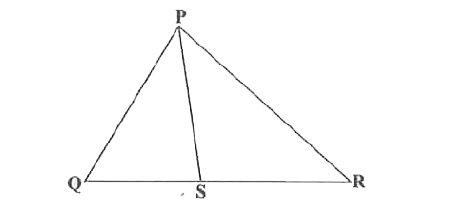 09:45View Solution
09:45View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π
04:04View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π .
01:52View SolutionA solid is in the form of a cone standing on a hemisphere with both their radii being equal to 8 cm and the height of cone is equal to its radius . Find the volume of solid.
02:50View Solutionएक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 सेमी है तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है | इस ठोस का आयतन π के पदों में ज्ञात कीजिए |
01:43View Solutionएक ठोस एक शंकु के आकार का है जो कि एक अर्धगोले पर रखा हुआ है और दोनों की त्रिज्याएँ 1 सेमी हैं तथा शंकु की ऊँचाई इसकी त्रिज्या के बराबर है। इस ठोस का आयतन तथा पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
02:53View Solutionएक ठोस एक अर्द्धगोले के ऊपर समान त्रिज्या 8 सेमी के शंकु के रूप में है और शंकु की ऊंचाई इसकी त्रिज्या के बराबर है ठोस का आयतन ज्ञात कीजिए ।
02:33View Solutionएक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिसकी त्रिज्याएँ 1 सेमी है तथा शंकु की ऊंचाई उसकी त्रिज्या के बराबर है । इस ठोस का आयतन π के पदों में ज्ञात कीजिए ।
01:58View SolutionA solid sphere of radius r melted and recast into the shape of a solid cone of height r, then radius of the base of the cone is (of equal volume)
03:23View SolutionA solid in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
04:44View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
04:06View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius.. Find the volume of the solid in terms of π.
05:37View Solution

