A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find the volume of the solid in terms of pi .
The correct Answer is:512πcm3
To find the volume of the solid formed by a cone standing on a hemisphere, we can break the problem down into a few steps.
1. Identify the dimensions:
- The radius of both the cone and the hemisphere is given as r=8 cm.
- The height of the cone is equal to its radius, so h=8 cm.
2. Calculate the volume of the cone:
- The formula for the volume of a cone is:
Vcone=13πr2h
- Substituting the values:
Vcone=13π(8)2(8)=13π(64)(8)=13π(512)=5123π cm3
3. Calculate the volume of the hemisphere:
- The formula for the volume of a hemisphere is:
Vhemisphere=23πr3
- Substituting the radius:
Vhemisphere=23π(8)3=23π(512)=10243π cm3
4. Calculate the total volume of the solid:
- The total volume Vtotal is the sum of the volumes of the cone and the hemisphere:
Vtotal=Vcone+Vhemisphere=5123π+10243π
- Combining the volumes:
Vtotal=(512+10243)π=15363π=512π cm3
Final Answer:
The volume of the solid in terms of π is:
512π cm3
- The radius of both the cone and the hemisphere is given as r=8 cm.
- The height of the cone is equal to its radius, so h=8 cm.
- The formula for the volume of a cone is:
Vcone=13πr2h
- Substituting the values:
Vcone=13π(8)2(8)=13π(64)(8)=13π(512)=5123π cm3
- The formula for the volume of a hemisphere is:
Vhemisphere=23πr3
- Substituting the radius:
Vhemisphere=23π(8)3=23π(512)=10243π cm3
- The total volume Vtotal is the sum of the volumes of the cone and the hemisphere:
Vtotal=Vcone+Vhemisphere=5123π+10243π
- Combining the volumes:
Vtotal=(512+10243)π=15363π=512π cm3
The volume of the solid in terms of π is:
512π cm3
Topper's Solved these Questions
Similar Questions
A solid is in the form of a cone standing on a hemisphere with both their radii being equal to 8 cm and the height of cone is equal to its radius . Find the volume of solid.
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
View SolutionA solid is in the shape of a cone surmounted on a hemi-sphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π=22/7 )
View SolutionThe height of a cone is 7 cm and its radius of base is 3 cm. Find its volume.
View SolutionA solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is 3.5cm and the height of the cone is 4cm. The solid is placed in a cylindrical tub, full of water, in such a way that the whole solid is submerged in water. If the radius of the cylinder is 5cm and its height is 10.5cm, find the volume of water left in the cylindrical tub. (Useπ=227)
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View SolutionThe base radius and slant height of a cone are 8 cm and 2√13cm respectively. Find the volume of the cone.
View SolutionA cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
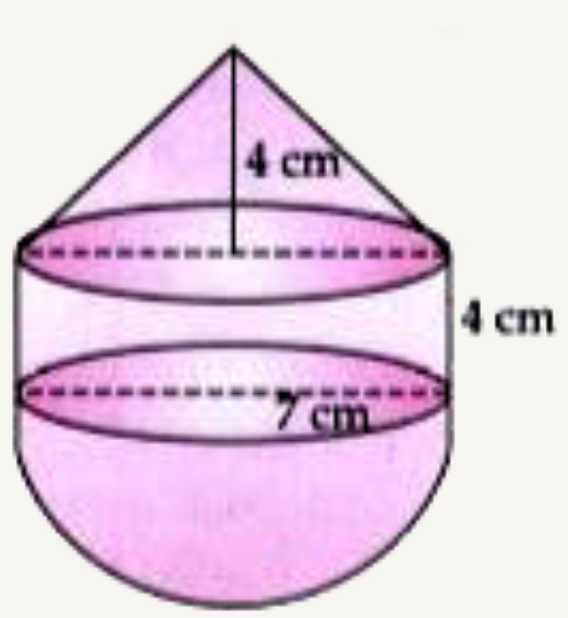
View SolutionThe following figure represents a solid consiting of right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.
 View Solution
View Solution

