At any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
v>0,a>0
v<0,a>0
v>0,a<0
v>0,a=0
The correct Answer is:A
To determine when the speed of a particle moving along a straight line is increasing, we need to analyze the relationship between velocity (v) and acceleration (a).
1. Understanding Speed and Velocity:
- Speed is the magnitude of velocity. If the velocity of the particle is positive, the speed is also increasing if the velocity increases.
- If the velocity is negative, the speed is still increasing if the absolute value of the velocity is increasing (i.e., moving further away from zero).
2. Acceleration Definition:
- Acceleration (a) is defined as the rate of change of velocity with respect to time, mathematically expressed as:
a=dvdt
- This means that acceleration indicates how the velocity is changing over time.
3. Condition for Increasing Speed:
- The speed of the particle is increasing if the velocity and acceleration have the same sign.
- This can be broken down into two cases:
- Case 1: If the velocity (v) is positive and acceleration (a) is also positive, the speed is increasing.
- Case 2: If the velocity (v) is negative and acceleration (a) is also negative, the speed is increasing (since the particle is moving in the negative direction but speeding up).
4. Conclusion:
- Therefore, we can summarize that the speed of the particle is increasing if:
v>0anda>0orv<0anda<0
- In simpler terms, the speed is increasing if:
v⋅a>0
- Speed is the magnitude of velocity. If the velocity of the particle is positive, the speed is also increasing if the velocity increases.
- If the velocity is negative, the speed is still increasing if the absolute value of the velocity is increasing (i.e., moving further away from zero).
- Acceleration (a) is defined as the rate of change of velocity with respect to time, mathematically expressed as:
a=dvdt
- This means that acceleration indicates how the velocity is changing over time.
- The speed of the particle is increasing if the velocity and acceleration have the same sign.
- This can be broken down into two cases:
- Case 1: If the velocity (v) is positive and acceleration (a) is also positive, the speed is increasing.
- Case 2: If the velocity (v) is negative and acceleration (a) is also negative, the speed is increasing (since the particle is moving in the negative direction but speeding up).
- Therefore, we can summarize that the speed of the particle is increasing if:
v>0anda>0orv<0anda<0
- In simpler terms, the speed is increasing if:
v⋅a>0
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)
33 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)
37 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE
30 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
4 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
Knowledge Check
A particle is moving along a straight line.
AIf the acceleration of the particle is more than that of another object, the particle is moving faster.BIf the acceleration is positive, the speed must be increasing.CIf the acceleration and the velocity have the same sign, the speed must be increasing.DIf the acceleration is zero, the velocity is constant but the speed may be changing.If a particle is moving along straight line with increasing speed, then
AIts acceleration is negativeBIts acceleration may be decreașingCIts acceleration is positiveDBoth (2) & (3)The velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :
 A23ms−2B−23ms−2C203ms−2D−203ms−2
A23ms−2B−23ms−2C203ms−2D−203ms−2
The variation of velocity of a particle moving along a straight line is shown in . is
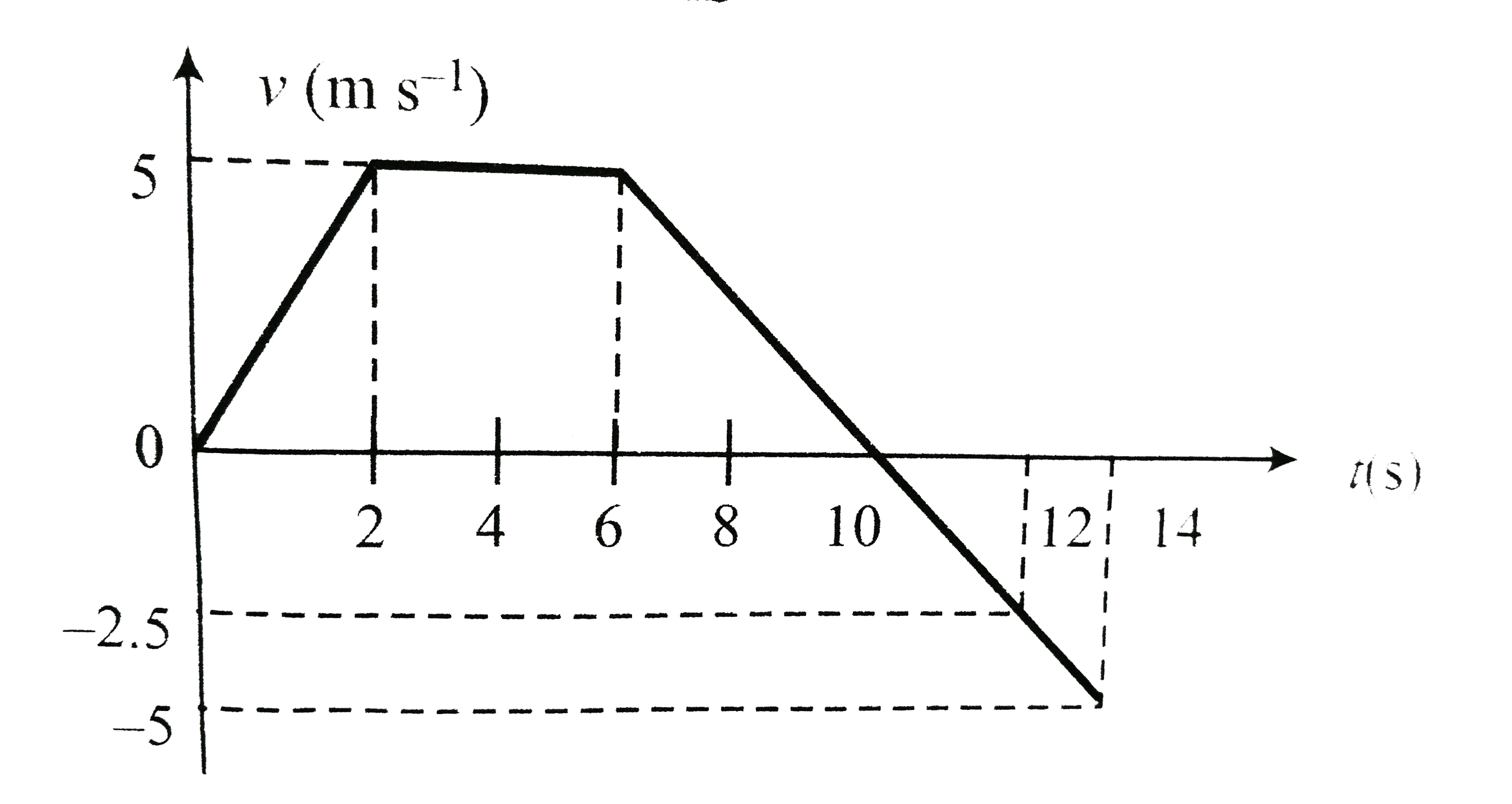 .
.
View SolutionThe figure shows a velocity-time graph of a particle moving along a straight line
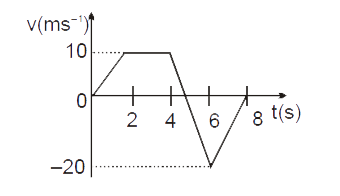
The maximum of displacement of the particle is
View SolutionThe figure shows a velocity-time graph of a particle moving along a straight line

Q. The maximum of displacement of the particle is
View Solution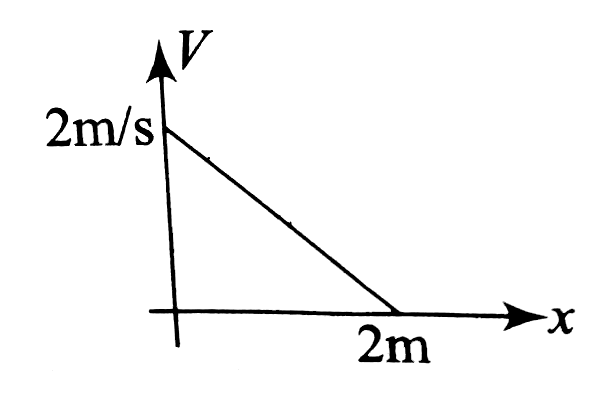
The velocity displacement graph of a particle moving along a straight line is shown in figure.
Then the acceleration displacement graph is.
View SolutionThe velocity-time graph of a particle moving along a straight line is given as below. The displacement time curve for the particle is given by :

View Solution