The position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
a=Ax
a=−ω2x
a=Aωx
a=ω2xA
The correct Answer is:B
To solve the problem, we need to find the expression for the acceleration a of a particle whose position x varies with time t as given by the equation:
x=Asin(ωt)
where A and ω are positive constants.
Step 1: Find the Velocity
The velocity v of the particle is the rate of change of position with respect to time. We can find it by differentiating x with respect to t:
v=dxdt
Using the chain rule, we differentiate x=Asin(ωt):
v=Addt(sin(ωt))=Acos(ωt)⋅ddt(ωt)=Aωcos(ωt)
Step 2: Find the Acceleration
The acceleration a of the particle is the rate of change of velocity with respect to time. We can find it by differentiating v with respect to t:
a=dvdt
Differentiating v=Aωcos(ωt):
a=Aωddt(cos(ωt))=Aω(−sin(ωt))⋅ddt(ωt)=−Aω2sin(ωt)
Step 3: Express Acceleration in Terms of Position x
From the original position equation x=Asin(ωt), we can express sin(ωt) in terms of x:
sin(ωt)=xA
Now, substituting this back into the acceleration equation:
a=−Aω2(xA)
This simplifies to:
a=−ω2x
Final Result
Thus, the acceleration a of the particle varies with its position x as:
a=−ω2x
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - B)
Explore 33 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - C)
Explore 37 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:EXERCISE
Explore 30 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Assignement section -J (Aakash Challengers Questions)
Explore 4 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - J)
Explore 2 Videos
Similar Questions
The position of a particle moving along x-axis varies with time t according to equation x=√3sinωt−cosωt where ω is constants. Find the refion in which the particle is confined.
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View Solution
Knowledge Check
The position of a particle moving along x- axis is given by x=x0cos2(ωt) . Its when it is at mean position is
A2x0ωBx0ω2Cx0ω2Dx0ωThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is
 A3m/s2B−5m/s2C−4m/s2D2.5m/s2
A3m/s2B−5m/s2C−4m/s2D2.5m/s2Position of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
AVelocity (i.edxdt) of particleBInitial velocity(i.edxdt att=0)CVelocity at t=2secDAccleration(i.ed2xdt2) of particle
The position of a particle moving along X -axis varies with time as x=ut+A sin omega t Att =0 x=0 . Between t=0 and t=t_(0) average velocity of particle is u .Then values of t_(0) can be
View SolutionThe position of a particle moving along X -axis varies with time as x=ut+A sin omega t. Att =0 x=0 . Between t=0 and t=t_(0) average velocity of particle is u .Then values of t_(0) can be (A) (A)/(u) (B) (pi)/(omega) (C) (2 pi)/(omega)
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
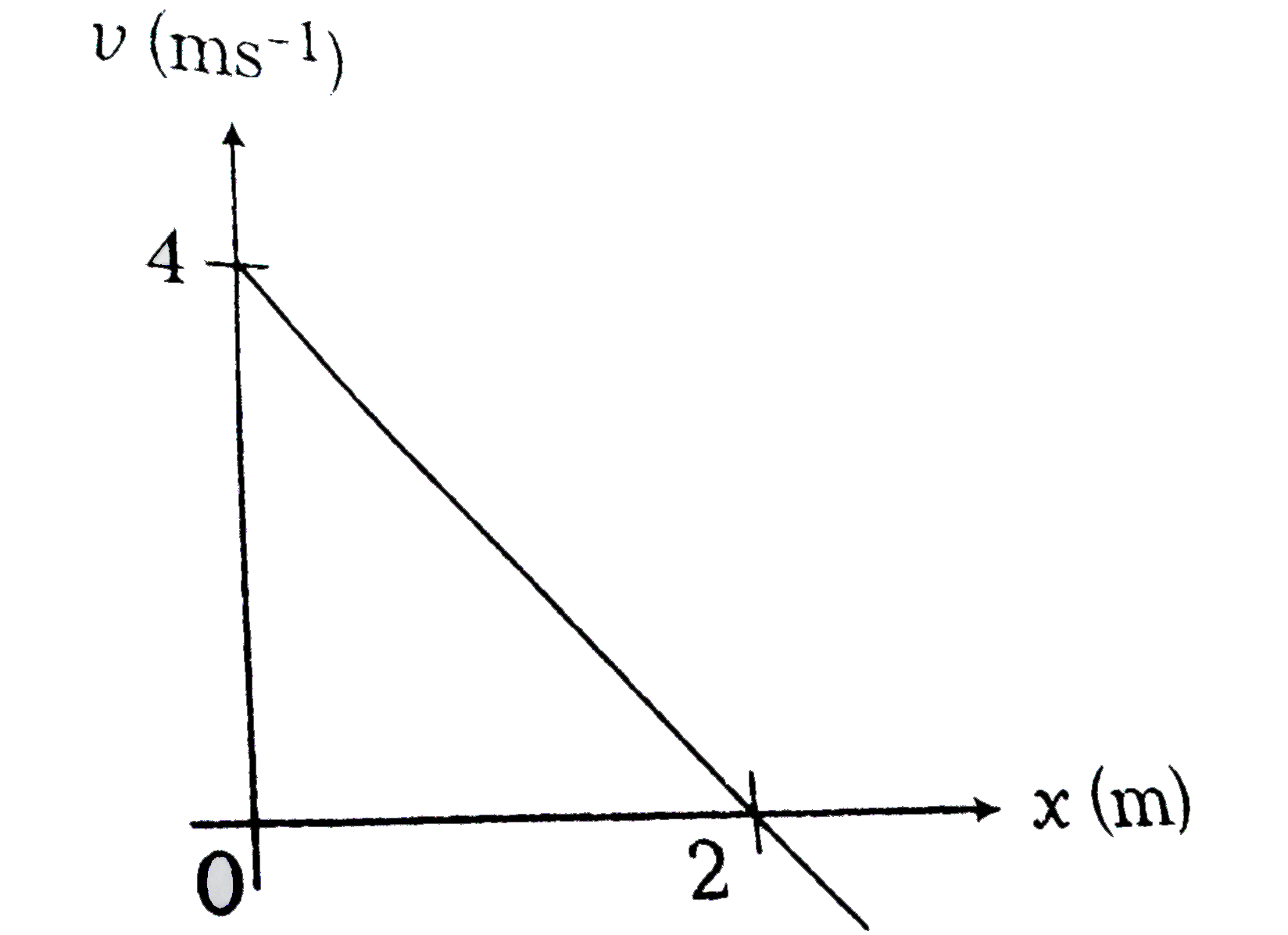
View SolutionThe position-time relation of a particle moving along the x-axis is given by
x=a−bt+ct2
where a, b and c are positive numbers. The velocity-time graph of the particle is
View SolutionA point moves in the plane y according to the law x=Asinωt,y=Bcosωt, whereA,B&ω are positive constant.
The acceleration of particle is given by [∵¯r is position vector]
View Solution