A particle is thrown with any velocity vertically upward, the distance travelled by the particle in first second of its decent is
g
g2
g4
Cannot be calculated
The correct Answer is:B
To find the distance traveled by a particle in the first second of its descent after being thrown vertically upward, we can use the equations of motion. Here's a step-by-step solution:
Step 1: Understand the Motion
When a particle is thrown vertically upward, it will rise until it reaches its maximum height, where its velocity becomes zero. After reaching this point, it will start descending. The distance traveled during the first second of descent is what we need to calculate.
Step 2: Identify Initial Conditions
At the moment the particle starts its descent:
- The initial velocity (u) at the start of the descent is 0 m/s (as it is at the peak).
- The time (t) for which we want to calculate the distance is 1 second.
- The acceleration due to gravity (g) is approximately 9.8 m/s² (we can use 10 m/s² for simplicity in calculations).
Step 3: Use the Second Equation of Motion
The second equation of motion states:
s=ut+12gt2
Where:
- s = distance traveled
- u = initial velocity
- g = acceleration due to gravity
- t = time
Step 4: Substitute the Values
Since the initial velocity u=0 (at the peak), the equation simplifies to:
s=0⋅t+12gt2
s=12g(12)
s=12g
Step 5: Calculate the Distance
Substituting g=10m/s2:
s=12⋅10
s=5m
Conclusion
The distance traveled by the particle in the first second of its descent is 5 meters.
---
When a particle is thrown vertically upward, it will rise until it reaches its maximum height, where its velocity becomes zero. After reaching this point, it will start descending. The distance traveled during the first second of descent is what we need to calculate.
At the moment the particle starts its descent:
- The initial velocity (u) at the start of the descent is 0 m/s (as it is at the peak).
- The time (t) for which we want to calculate the distance is 1 second.
- The acceleration due to gravity (g) is approximately 9.8 m/s² (we can use 10 m/s² for simplicity in calculations).
The second equation of motion states:
s=ut+12gt2
Where:
- s = distance traveled
- u = initial velocity
- g = acceleration due to gravity
- t = time
Since the initial velocity u=0 (at the peak), the equation simplifies to:
s=0⋅t+12gt2
s=12g(12)
s=12g
Substituting g=10m/s2:
s=12⋅10
s=5m
The distance traveled by the particle in the first second of its descent is 5 meters.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)33videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)37videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE30videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)4videos
MOTION IN A PLANE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)2videos
MOTION IN STRAIGHT LINE
Similar Questions
A particle is thrown vertically upward with speed 45m/s. Find the distance covered by the particle in the 5th second of its journey.
View SolutionA particle is projected vertically upward and moves freely under gravity.If the distance travelled by the particle in the 4th second of its motion is twice of that in the 5th second,then the speed of projection is ?[g=10m/s2]
View Solution
Knowledge Check
- Question 1 - Select One
A particle is thrown up with an initial velocity such that it takes more than one second to reach the top point. What is the distance travelled by the particle during the first second of its decent?
Ag/2Bg/4CgDInformation is insufficient to calculate the desired distance. - Question 2 - Select One
If S=3t3+9t2+2t+7 , then distance travelled by the particle during the first second of its motion is
A7 unitsB21 unitsC14 unitsD28 units - Question 3 - Select One
A ball is thrown vertically upwards with a speed 70m/s. The distance travelled by theball in its seventh second of motion will be [g=10m/s2]
A10mB2.1mC3.4D5m
A particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
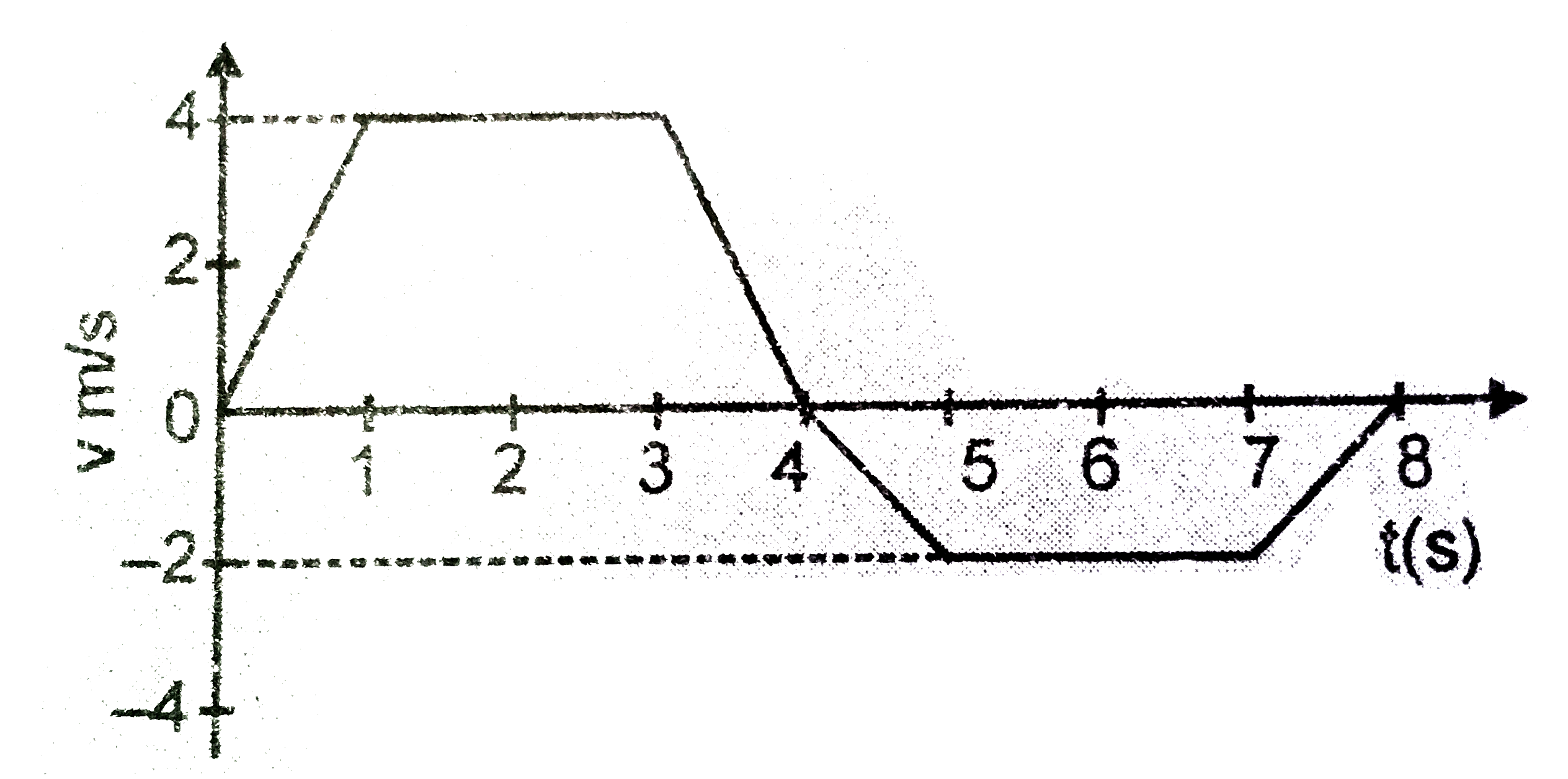 View Solution
View SolutionThe velocity of a particle varies with time as per the figure shown. The distance travelled by the particle in 10 seconds is ?(m/s)
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionIf a ball is thrown vertically upwards with speed u, the distance covered during the last t second of its ascent is
View SolutionIf a ball is thrown vertically upwards with speed u, the distance covered during the last t second of its ascent is
View Solution

