For a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
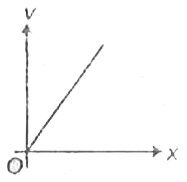
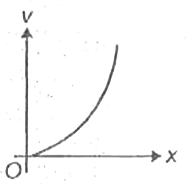
The correct Answer is:C
To solve the problem of how the velocity (v) of a body moving with uniform acceleration varies with its position (x), we can follow these steps:
Step 1: Understand the relationship between acceleration, velocity, and position.
For a body moving with uniform acceleration, we know that acceleration (a) is constant. The relationship between velocity (v), acceleration (a), and position (x) can be derived from the basic kinematic equations.
Step 2: Use the definition of acceleration.
Acceleration is defined as the rate of change of velocity with respect to time:
a=dvdt
Step 3: Express acceleration in terms of velocity and position.
Using the chain rule, we can express acceleration in terms of velocity and position:
a=dvdt=dvdx⋅dxdt=vdvdx
Thus, we can rewrite the acceleration as:
a=vdvdx
Step 4: Relate acceleration to the change in velocity.
Since acceleration is constant, we can set it equal to a constant value (let's denote it as C):
vdvdx=C
Step 5: Rearrange and integrate.
Rearranging gives us:
vdv=Cdx
Now, we can integrate both sides. The left side integrates from the initial velocity 0 to v, and the right side integrates from the initial position 0 to x:
∫v0vdv=∫x0Cdx
Step 6: Perform the integration.
The left side becomes:
v22∣∣v0=v22
The right side becomes:
Cx∣∣x0=Cx
Thus, we have:
v22=Cx
Step 7: Solve for velocity.
Multiplying both sides by 2 gives:
v2=2Cx
Step 8: Identify the relationship.
This equation v2=2Cx indicates that the relationship between velocity and position is quadratic. If we rearrange it, we can express it as:
v2=2Cx
This is similar to the standard form of a parabola y2=4Ax, where A is a constant.
Conclusion:
The variation of velocity (v) with position (x) for a body moving with uniform acceleration is best represented by a parabolic curve, specifically v2 as a function of x.
---
For a body moving with uniform acceleration, we know that acceleration (a) is constant. The relationship between velocity (v), acceleration (a), and position (x) can be derived from the basic kinematic equations.
Acceleration is defined as the rate of change of velocity with respect to time:
a=dvdt
Using the chain rule, we can express acceleration in terms of velocity and position:
a=dvdt=dvdx⋅dxdt=vdvdx
Thus, we can rewrite the acceleration as:
a=vdvdx
Since acceleration is constant, we can set it equal to a constant value (let's denote it as C):
vdvdx=C
Rearranging gives us:
vdv=Cdx
Now, we can integrate both sides. The left side integrates from the initial velocity 0 to v, and the right side integrates from the initial position 0 to x:
∫v0vdv=∫x0Cdx
The left side becomes:
v22∣∣v0=v22
The right side becomes:
Cx∣∣x0=Cx
Thus, we have:
v22=Cx
Multiplying both sides by 2 gives:
v2=2Cx
This equation v2=2Cx indicates that the relationship between velocity and position is quadratic. If we rearrange it, we can express it as:
v2=2Cx
This is similar to the standard form of a parabola y2=4Ax, where A is a constant.
The variation of velocity (v) with position (x) for a body moving with uniform acceleration is best represented by a parabolic curve, specifically v2 as a function of x.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)33videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)37videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE30videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)4videos
MOTION IN A PLANE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)2videos
MOTION IN STRAIGHT LINE
Similar Questions
Mark the statement true (T) or false (F). For a particle moving with a constant acceleration along a straight line, the velocity- time graph is a straight line.
View SolutionA particle is moving with uniform acceleration along a straight line "ABC" .Its velocity at A and B are 6m/s" and "9m/s respectively. If AB:BC=5:16" then its velocity at C is
View Solution
Knowledge Check
- Question 1 - Select One
A body is moving with uniform acceleration. Its 'velocity
Awill be increasing,Bwill be decreasing,Cwill be uniform,Dwill increase first and decrease afterward. - Question 2 - Select One
A body A starts from rest and moves with a uniform acceleration along a straight line. Another body B has some initial velocity and moves with larger acceleration than that of A. The correct velocity time graphs
A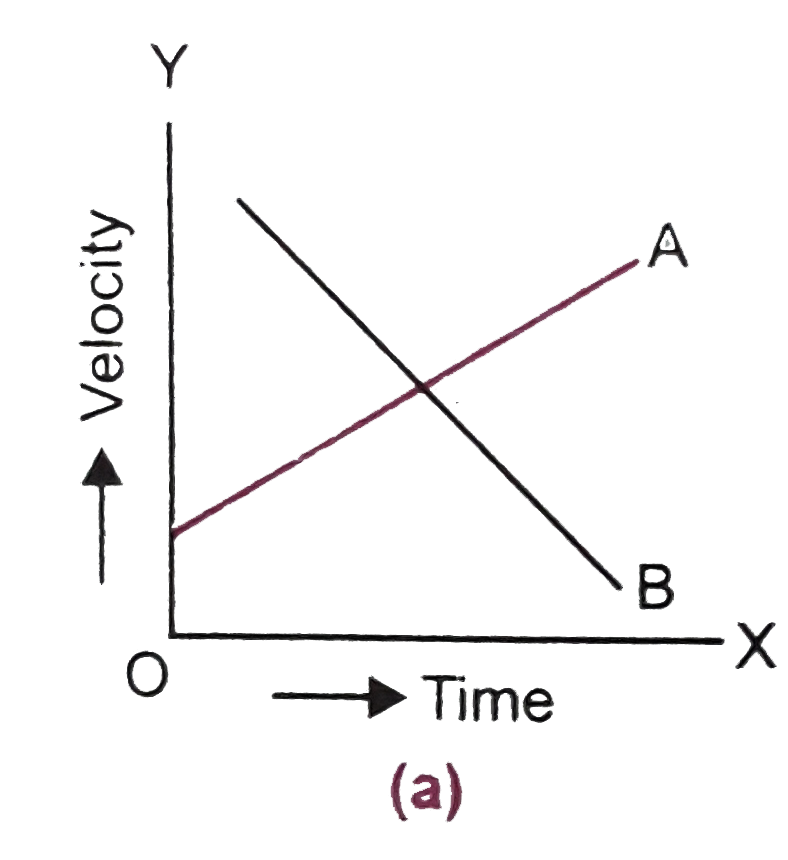 B
B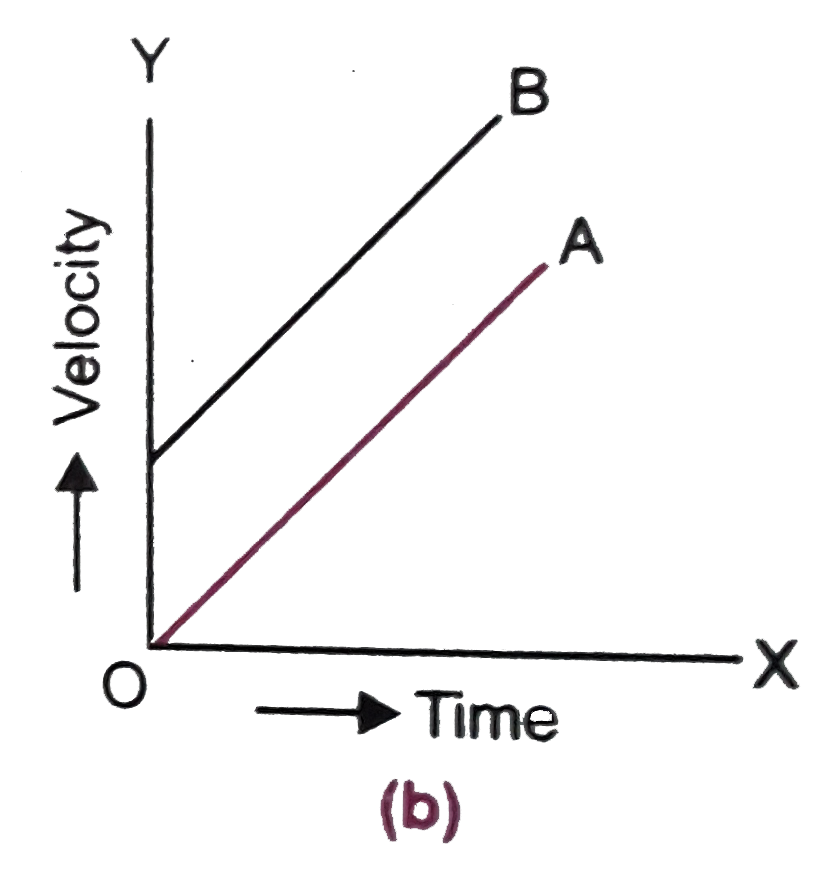 C
C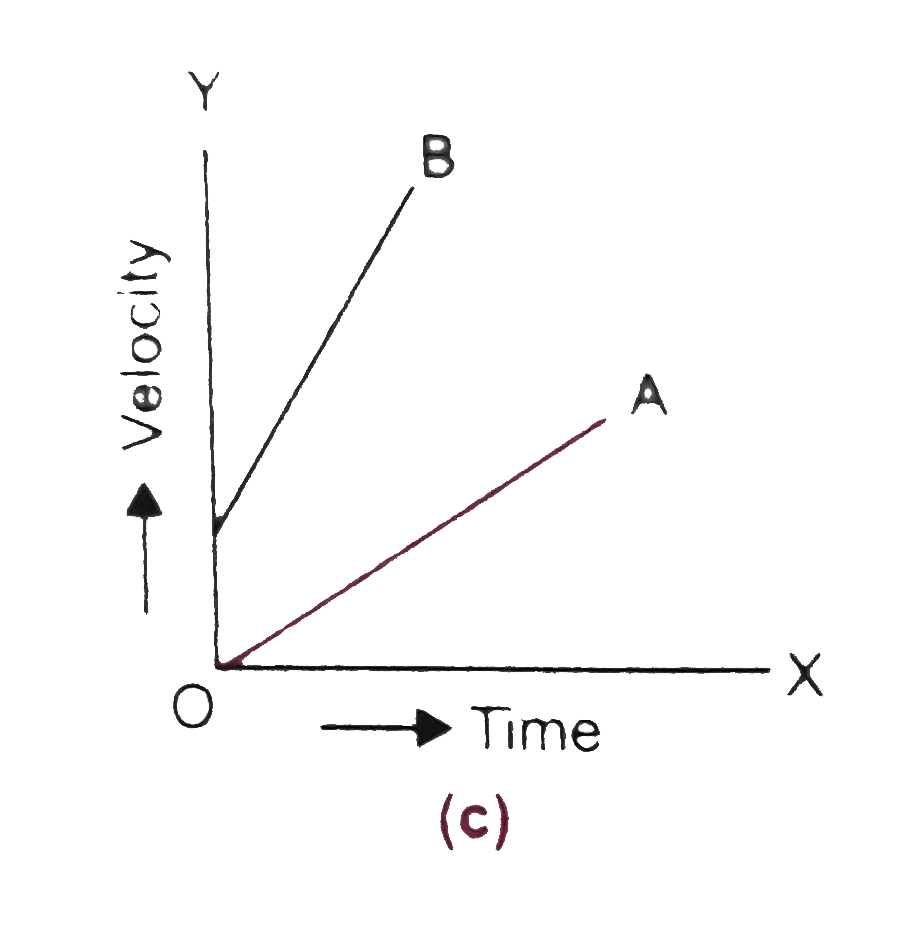 D
D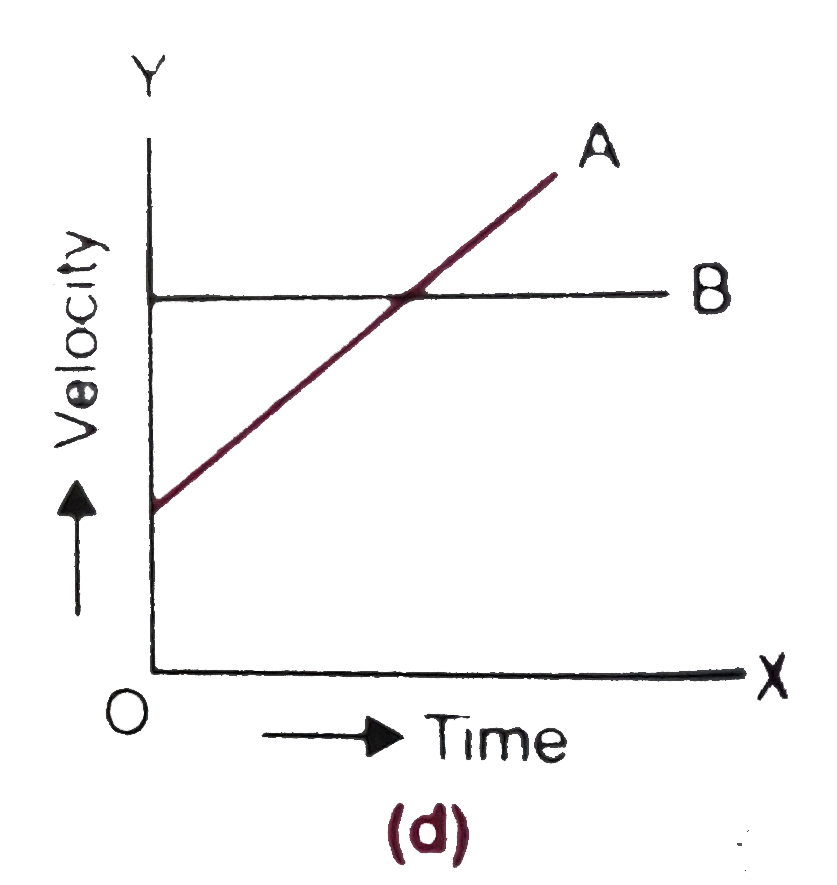
- Question 3 - Select One
A body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph
A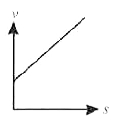 B
B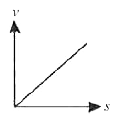 C
C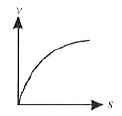 D
D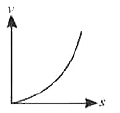
A particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
 .View Solution
.View SolutionA body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph
View SolutionA particle is moving with uniform acceleration along a straight line ABC. Its velocity at A and B are 6 m/s and 9 m/s respectively if AB:BC=5:16 then its velocity at C is
View SolutionA body starting from rest moves along a string line with a constant acceleration The variation of speed (v) with distance (s) is repressed by the graph
View SolutionAn object is moving with uniform acceleration a. Its initial velocity is u and after time t its velocity is v. The equation of its motion is v = u + at. The velocity (along y-axis) time (along x-axis) graph shall be a straight line
View Solution

