An object is moving with uniform acceleration a. Its initial velocity is u and after time t its velocity is v. The equation of its motion is v = u + at. The velocity (along y-axis) time (along x-axis) graph shall be a straight line
passing through origin
with x-intercept u
with y-intercept u
with slope u
The correct Answer is:C
To solve the problem step by step, we will analyze the motion of an object with uniform acceleration and derive the corresponding velocity-time graph.
Step 1: Understand the given equation
The equation of motion for an object moving with uniform acceleration is given by:
v=u+at
where:
- v = final velocity
- u = initial velocity
- a = acceleration
- t = time
Step 2: Identify the variables for the graph
In this scenario, we will plot:
- The y-axis will represent the velocity v.
- The x-axis will represent the time t.
Step 3: Rearrange the equation
We can rearrange the equation v=u+at to fit the form of a straight line equation y=mx+c:
- Here, v (velocity) is the dependent variable (y-axis).
- t (time) is the independent variable (x-axis).
- The equation can be rewritten as:
v=at+u
This shows that:
- The slope m of the line is equal to the acceleration a.
- The y-intercept c is equal to the initial velocity u.
Step 4: Graph the equation
Now, we can sketch the graph:
- Start by plotting the y-intercept u on the y-axis.
- Since the slope is a, for every unit increase in t, v increases by a.
- Draw a straight line starting from the point (0,u) and extending upwards with a slope of a.
Step 5: Analyze the graph
The graph will be a straight line:
- The slope of the line represents the acceleration a.
- The point where the line intersects the y-axis represents the initial velocity u.
Conclusion
Thus, the velocity-time graph for an object moving with uniform acceleration is a straight line with:
- Slope = a (acceleration)
- Y-intercept = u (initial velocity)
The equation of motion for an object moving with uniform acceleration is given by:
v=u+at
where:
- v = final velocity
- u = initial velocity
- a = acceleration
- t = time
In this scenario, we will plot:
- The y-axis will represent the velocity v.
- The x-axis will represent the time t.
We can rearrange the equation v=u+at to fit the form of a straight line equation y=mx+c:
- Here, v (velocity) is the dependent variable (y-axis).
- t (time) is the independent variable (x-axis).
- The equation can be rewritten as:
v=at+u
This shows that:
- The slope m of the line is equal to the acceleration a.
- The y-intercept c is equal to the initial velocity u.
Now, we can sketch the graph:
- Start by plotting the y-intercept u on the y-axis.
- Since the slope is a, for every unit increase in t, v increases by a.
- Draw a straight line starting from the point (0,u) and extending upwards with a slope of a.
The graph will be a straight line:
- The slope of the line represents the acceleration a.
- The point where the line intersects the y-axis represents the initial velocity u.
Thus, the velocity-time graph for an object moving with uniform acceleration is a straight line with:
- Slope = a (acceleration)
- Y-intercept = u (initial velocity)
Topper's Solved these Questions
Similar Questions
.An object is moving with a uniform acceleration which is parallel to its instantaneous direction of motion.The displacement x - velocity (v) graph of this object is
View SolutionFor a body moving withuniform acceleration 'a', initial and final velocities in a time interval are 'u' and respectively.Then,its average velocity in the time interval T is
View Solution
Knowledge Check
For body moving with uniform acceleration a, initial and final velocities in a time interval t are u and v respectively. Then its average velocity in the time interval t is
A(v+at)B(v−at2)C(v−at)D(u−at2)For a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
A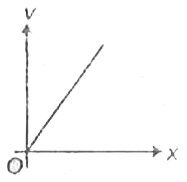 B
B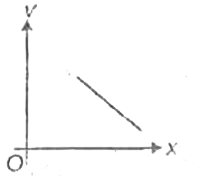 C
C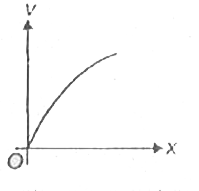 D
D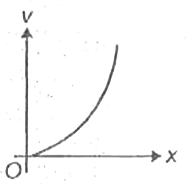
At the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity v after time t, is
Av=u+atBv=u+at2Cv=u+12at2Dv=at2
At the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity v after timet, is
View SolutionAt the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity vafter time t, is
View SolutionAn object is moving with a uniform acceleration which is parallel to its instantaneous direction of motion. The dispalcement (s)-velocity (v) graph of this object is.
View SolutionA particle is moving along X-axis Its acceleration at time t is proportional to its velocity at that time. The differential equation of the motion of the particle is
View SolutionVelocity of a body moving a straight line with uniform acceleration (a) reduces by 34 of its initial velocity in time t0. The total time of motion of the body till its velocity becomes zero is
View Solution
