According to Newton's 2nd law of motion correct equation is (where symbols have their usual meanings)
All of these
To solve the question regarding Newton's 2nd law of motion, we will derive the equation step by step.
1. Understanding Newton's 2nd Law:
Newton's 2nd law states that the force acting on an object is equal to the rate of change of its momentum. Mathematically, this can be expressed as:
F=dpdt
where F is the force, p is the momentum, and t is time.
Hint: Remember that momentum p is defined as the product of mass m and velocity v: p=mv.
2. Expressing Momentum:
The momentum p can be expressed as:
p=mv
Therefore, we can rewrite the force equation as:
F=d(mv)dt
Hint: Keep in mind that m can be constant or variable, which will affect how we differentiate.
3. Applying the Product Rule:
If we apply the product rule of differentiation to mv, we get:
F=mdvdt+vdmdt
Here, dvdt is the acceleration a of the object.
Hint: The product rule states that if you have two functions multiplied together, the derivative is the derivative of the first times the second plus the first times the derivative of the second.
4. Considering Constant Mass:
If the mass m is constant, then dmdt=0. Thus, the equation simplifies to:
F=mdvdt=ma
Hint: This is the most common form of Newton's second law, where force is equal to mass times acceleration.
5. Considering Variable Mass:
If the mass is not constant, then we must consider both terms:
F=mdvdt+vdmdt
This indicates that the force can also arise from changes in mass, such as in rocket propulsion.
Hint: Think about how rockets expel gas to change mass while accelerating.
6. Conclusion:
Therefore, the correct equations according to Newton's second law of motion can be summarized as:
- For constant mass: F=ma
- For variable mass: F=mdvdt+vdmdt
Hint: Both forms of the equation are valid under different conditions regarding mass.
Final Answer:
The correct equations according to Newton's 2nd law of motion are:
1. F=ma (for constant mass)
2. F=mdvdt+vdmdt (for variable mass)
Newton's 2nd law states that the force acting on an object is equal to the rate of change of its momentum. Mathematically, this can be expressed as:
F=dpdt
where F is the force, p is the momentum, and t is time.
The momentum p can be expressed as:
p=mv
Therefore, we can rewrite the force equation as:
F=d(mv)dt
If we apply the product rule of differentiation to mv, we get:
F=mdvdt+vdmdt
Here, dvdt is the acceleration a of the object.
If the mass m is constant, then dmdt=0. Thus, the equation simplifies to:
F=mdvdt=ma
If the mass is not constant, then we must consider both terms:
F=mdvdt+vdmdt
This indicates that the force can also arise from changes in mass, such as in rocket propulsion.
Therefore, the correct equations according to Newton's second law of motion can be summarized as:
- For constant mass: F=ma
- For variable mass: F=mdvdt+vdmdt
The correct equations according to Newton's 2nd law of motion are:
1. F=ma (for constant mass)
2. F=mdvdt+vdmdt (for variable mass)
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)65videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)44videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Example24videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions10videos
KINETIC THEORY
- BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)26videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
According to Newton second law of motion
AF=m×vBf=m×aCf=maDf=mv - Question 2 - Select One
The correct combination is (symbols have their usual meanings)
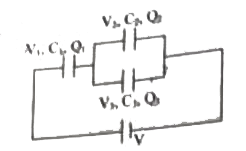 AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3 - Question 3 - Select One
Select the incorrect relation. (Where symboles have their usual meanings):-
ACp=γRγ−1BCP−CV=RCΔU=PfVf−PiVi1−γDCv=Rγ−1
Newton's Laws of Motion
View SolutionWhat are Newton's laws of motion?
View SolutionSelect the incorrect relation. (Where symboles have their usual meanings):-
View SolutionBohr magnetonis given by (symbols have their usual meanings)
View SolutionChoose the correct arrangement, where the symbols have their usual meanings
View Solution

