A particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
Zero
2mv
√3mv
mv
To solve the problem, we need to analyze the situation of a particle of mass m striking a wall elastically at an angle of 60∘ with an initial velocity v. We will calculate the change in momentum of the ball along the wall.
1. Identify the Components of Velocity:
The velocity v of the particle can be resolved into two components:
- Perpendicular to the wall: v⊥=vsin(60∘)
- Parallel to the wall: v∥=vcos(60∘)
2. Calculate the Components:
Using the trigonometric values:
- sin(60∘)=√32
- cos(60∘)=12
Thus,
v⊥=v⋅√32
v∥=v⋅12
3. Analyze the Elastic Collision:
In an elastic collision with a smooth wall, the component of velocity perpendicular to the wall will reverse direction, while the parallel component remains unchanged. Therefore:
- After the collision, the perpendicular component becomes −v⊥.
- The parallel component remains v∥.
4. Calculate the Change in Momentum:
The momentum before the collision in the perpendicular direction is:
p_{\perpendicular, \text{initial}} = m \cdot v_{\perp} = m \cdot v \cdot \frac{\sqrt{3}}{2}
The momentum after the collision in the perpendicular direction is:
p_{\perpendicular, \text{final}} = m \cdot (-v_{\perp}) = -m \cdot v \cdot \frac{\sqrt{3}}{2}
The change in momentum in the perpendicular direction is:
\Delta p_{\perpendicular} = p_{\perpendicular, \text{final}} - p_{\perpendicular, \text{initial}} = -m \cdot v \cdot \frac{\sqrt{3}}{2} - m \cdot v \cdot \frac{\sqrt{3}}{2} = -2m \cdot v \cdot \frac{\sqrt{3}}{2} = -m \cdot v \cdot \sqrt{3}
5. Change in Momentum Along the Wall:
Since there is no change in the parallel component of momentum (as the wall is smooth), the change in momentum along the wall is:
Δp∥=0
Final Result:
The magnitude of change in momentum of the ball along the wall is:
Δp∥=0
The velocity v of the particle can be resolved into two components:
- Perpendicular to the wall: v⊥=vsin(60∘)
- Parallel to the wall: v∥=vcos(60∘)
Using the trigonometric values:
- sin(60∘)=√32
- cos(60∘)=12
v⊥=v⋅√32
v∥=v⋅12
In an elastic collision with a smooth wall, the component of velocity perpendicular to the wall will reverse direction, while the parallel component remains unchanged. Therefore:
- After the collision, the perpendicular component becomes −v⊥.
- The parallel component remains v∥.
The momentum before the collision in the perpendicular direction is:
p_{\perpendicular, \text{initial}} = m \cdot v_{\perp} = m \cdot v \cdot \frac{\sqrt{3}}{2}
The momentum after the collision in the perpendicular direction is:
p_{\perpendicular, \text{final}} = m \cdot (-v_{\perp}) = -m \cdot v \cdot \frac{\sqrt{3}}{2}
\Delta p_{\perpendicular} = p_{\perpendicular, \text{final}} - p_{\perpendicular, \text{initial}} = -m \cdot v \cdot \frac{\sqrt{3}}{2} - m \cdot v \cdot \frac{\sqrt{3}}{2} = -2m \cdot v \cdot \frac{\sqrt{3}}{2} = -m \cdot v \cdot \sqrt{3}
Since there is no change in the parallel component of momentum (as the wall is smooth), the change in momentum along the wall is:
Δp∥=0
The magnitude of change in momentum of the ball along the wall is:
Δp∥=0
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Example
24 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
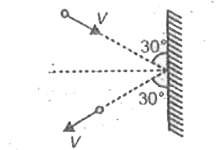
A particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
View SolutionA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View Solution
Knowledge Check
A particle of mass m strikes elastically against a wall at angle of incidence 60∘ with velocity v. The change in momentum is
AmvB2mvCmv2Dmv4A body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
A2 m vBm vC12mvD0A molecule of mass m moving at a velocity v impinges elastically on the wall at an angle a with the wall. Then
Athe impulsive reaction of the wall is 2mvcosαBthe impulsive reaction of the wall is 2mvsinαCthe impulsive reaction of the wall is nonzeroDgiven data is insufficient to calculate impulsive reaction of the wall
A 1kg particle strikes a wall with a velocity 1ms at an angle of 60°with the wall and reflects at the same angle.If it remains in contact with the wall for 0.1sec, then the force is
View SolutionA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60∘ with the wall and reflects at the same angle. If it remains in contact with wall for 0.1 s, then the force is
View SolutionA particle of mass M strikes a wall at an angle of incidence 60∘ with velocity V elastically Then the change in momentum is
View SolutionA ball of mass 'm' moves normal to a wall with a velocity 'u' and rebounds with the same speed. The change in momentum of the ball during the rebounding is
View SolutionA body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View Solution
