A block is stationary on a rough inclined plane. How many forces are acting on the block?
2
3
4
5
To determine how many forces are acting on a block that is stationary on a rough inclined plane, we can analyze the situation step by step.
1. Identify the Block and the Inclined Plane:
- Consider a block resting on a rough inclined plane. The block is stationary, which indicates that the forces acting on it are balanced.
2. Identify the Forces Acting on the Block:
- The first force acting on the block is its weight (W), which acts vertically downward. The weight can be expressed as W=mg, where m is the mass of the block and g is the acceleration due to gravity.
3. Resolve the Weight into Components:
- The weight can be resolved into two components relative to the inclined plane:
- Perpendicular Component: W⊥=mgcos(θ), acting perpendicular to the inclined plane.
- Parallel Component: W∥=mgsin(θ), acting parallel to the inclined plane, directed down the slope.
4. Identify the Normal Force:
- The inclined plane exerts a normal force (N) on the block, which acts perpendicular to the surface of the inclined plane. This normal force balances the perpendicular component of the weight:
- N=mgcos(θ).
5. Identify the Frictional Force:
- Since the block is stationary, there must be a frictional force (f) acting up the slope, opposing the motion that would be caused by the parallel component of the weight. This frictional force balances the parallel component of the weight:
- f=mgsin(θ).
6. Count the Forces:
- Now, we can count the distinct forces acting on the block:
- The weight of the block (W).
- The normal force (N).
- The frictional force (f).
- Thus, there are a total of three forces acting on the block.
Final Answer:
The total number of forces acting on the block is 3.
---
- Consider a block resting on a rough inclined plane. The block is stationary, which indicates that the forces acting on it are balanced.
- The first force acting on the block is its weight (W), which acts vertically downward. The weight can be expressed as W=mg, where m is the mass of the block and g is the acceleration due to gravity.
- The weight can be resolved into two components relative to the inclined plane:
- Perpendicular Component: W⊥=mgcos(θ), acting perpendicular to the inclined plane.
- Parallel Component: W∥=mgsin(θ), acting parallel to the inclined plane, directed down the slope.
- The inclined plane exerts a normal force (N) on the block, which acts perpendicular to the surface of the inclined plane. This normal force balances the perpendicular component of the weight:
- N=mgcos(θ).
- Since the block is stationary, there must be a frictional force (f) acting up the slope, opposing the motion that would be caused by the parallel component of the weight. This frictional force balances the parallel component of the weight:
- f=mgsin(θ).
- Now, we can count the distinct forces acting on the block:
- The weight of the block (W).
- The normal force (N).
- The frictional force (f).
- Thus, there are a total of three forces acting on the block.
The total number of forces acting on the block is 3.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Example
24 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block is placed on a rough horizontal plane. Three horizontalforces are applied on the block as shown in the figure. If the block is in equilibrium, find the friction force acting on the block.
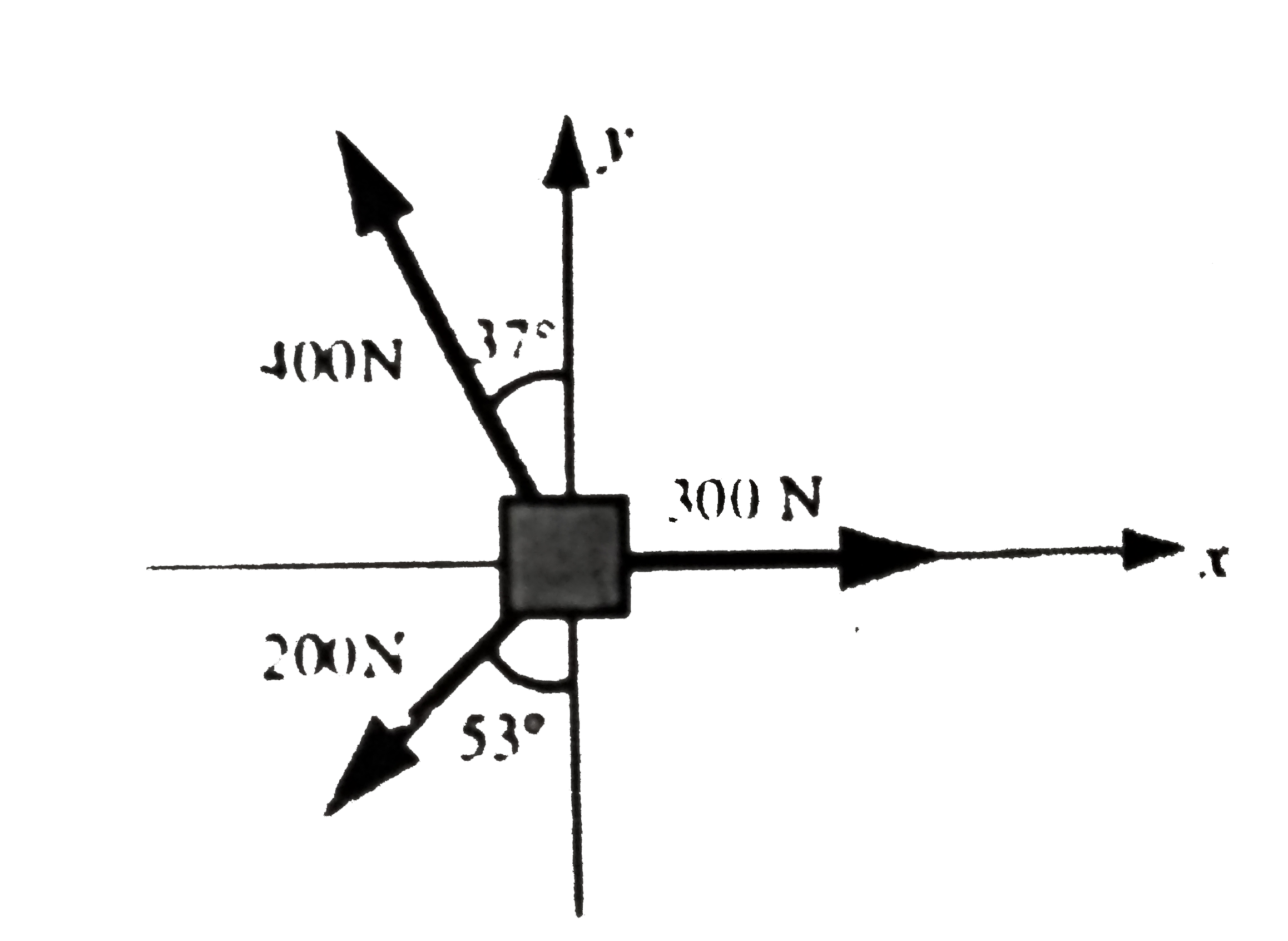
View Solution
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block of mass mm remains stationary on a fixed inclined plane of inclination θ . If μ= coefficient of static friction the reaction of ground on the block is:
AμgcosθBmgcosθCmgsinθDmg↓A block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
AZeroBgsinθ−μgcosθCgsinθ−μgcosθDNone of these
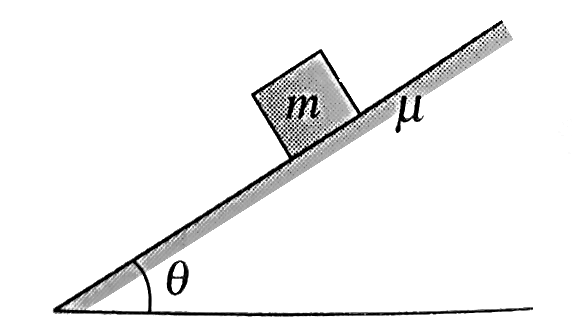A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:
View Solution
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. For what value of θ will the block slide on the inclined plane:
View Solution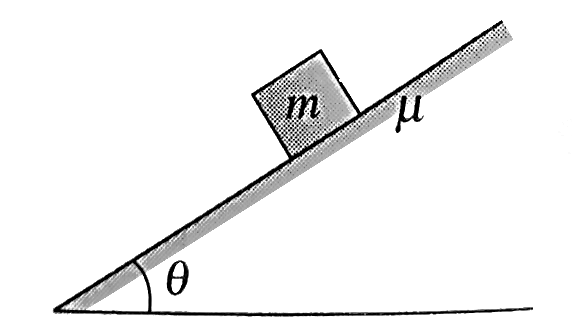
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If the entire system, were accelerated upward with acceleration a the angle of repose, would:
View SolutionA block of mass m is placed on a rough inclined plane. When the inclination of the plane is θ , the block just beging to slide down the plane under its own weight. The minimum force applied parallel to the plane, to move the block up the plane, is.
View SolutionA block is at rest at the top of a rough inclined plane of inclination 30° with the horizontal. What is the coefficient of kinetic friction between the block and the plane, if the . block slides down with an acceleration of g5 ?
View Solution