If the string of a conical pendulum makes an angle θ with horizontal, then square of its time period is proportional to
sinθ
cosθ
tanθ
cotθ
To solve the problem, we need to analyze the forces acting on a conical pendulum and derive the relationship between the time period and the angle θ.
1. Understanding the Conical Pendulum:
A conical pendulum consists of a mass attached to a string that swings in a horizontal circle while the string makes an angle θ with the vertical. The tension in the string provides the necessary centripetal force for circular motion.
2. Identifying Forces:
The forces acting on the mass are:
- The gravitational force mg acting downward.
- The tension T in the string acting along the string.
3. Resolving the Tension:
We can resolve the tension T into two components:
- Tcosθ acting vertically (balancing the weight).
- Tsinθ acting horizontally (providing the centripetal force).
4. Setting Up the Equations:
From the vertical balance of forces:
Tcosθ=mg(1)
From the horizontal component providing centripetal force:
Tsinθ=mv2r(2)
5. Dividing the Equations:
Dividing equation (2) by equation (1):
TsinθTcosθ=mv2rmg
This simplifies to:
tanθ=v2rg(3)
6. Finding the Radius r:
The radius r of the circular path can be expressed in terms of the length of the string l and the angle θ:
r=lsinθ
7. Substituting for r:
Substitute r back into equation (3):
tanθ=v2(lsinθ)g
Rearranging gives:
v2=lgsinθtanθ
8. Finding the Time Period T:
The time period T of the pendulum is given by:
T=2πrv
Substituting r=lsinθ:
T=2π(lsinθ)v
9. Substituting for v:
Substitute v2 from above into the time period equation:
T2=4π2(lsinθ)2lgsinθtanθ
Simplifying gives:
T2∝lsinθgtanθ
10. Final Relationship:
Since tanθ=sinθcosθ, we can express this as:
T2∝lsin2θgcosθ
Conclusion:
Thus, the square of the time period T2 is proportional to sin2θcosθ.
A conical pendulum consists of a mass attached to a string that swings in a horizontal circle while the string makes an angle θ with the vertical. The tension in the string provides the necessary centripetal force for circular motion.
The forces acting on the mass are:
- The gravitational force mg acting downward.
- The tension T in the string acting along the string.
We can resolve the tension T into two components:
- Tcosθ acting vertically (balancing the weight).
- Tsinθ acting horizontally (providing the centripetal force).
From the vertical balance of forces:
Tcosθ=mg(1)
From the horizontal component providing centripetal force:
Tsinθ=mv2r(2)
Dividing equation (2) by equation (1):
TsinθTcosθ=mv2rmg
This simplifies to:
tanθ=v2rg(3)
The radius r of the circular path can be expressed in terms of the length of the string l and the angle θ:
r=lsinθ
Substitute r back into equation (3):
tanθ=v2(lsinθ)g
Rearranging gives:
v2=lgsinθtanθ
The time period T of the pendulum is given by:
T=2πrv
Substituting r=lsinθ:
T=2π(lsinθ)v
Substitute v2 from above into the time period equation:
T2=4π2(lsinθ)2lgsinθtanθ
Simplifying gives:
T2∝lsinθgtanθ
Since tanθ=sinθcosθ, we can express this as:
T2∝lsin2θgcosθ
Thus, the square of the time period T2 is proportional to sin2θcosθ.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of σC/m2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle β with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
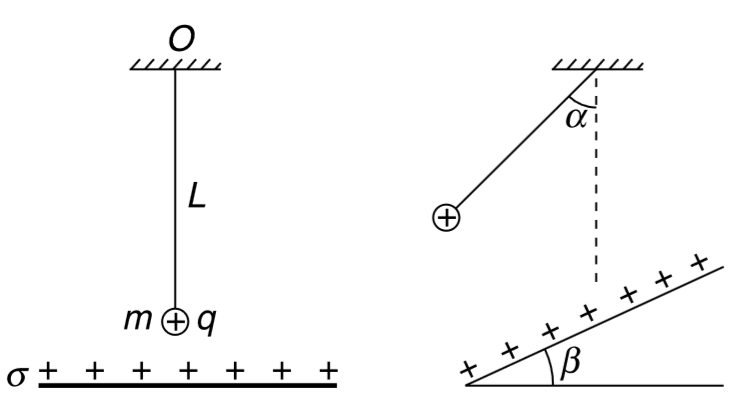
View SolutionWhen the string of a conical pendulum makes an angle of 45∘ with the vertical , its time is T1 when the string makes an angle of 60∘ with the vertical , its time period is T2 then T21/T22is
View Solution
Knowledge Check
A conical pendulum of length L makes an angle θ with the vertical. The time period will be
 A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√Lgtanθ
A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√LgtanθKepler's law of planetary motion states that the square of the time period is proportional to the
Asemi-major axisBsquare of the semi-major axisCcube of the semi-major axisDfourth power of the semi major axisKepler's law of planetary motion states that the square of the time period is proportional to the
Asemi-major axisBsquare of the semi-major axisCcube of the semi-major axisDfourth power of the semi-major axis
A simple pendulum is set up on a trolley which slides down a frictionless inclined plane making an angle θ with horizontal. The time period of pendulum is
View SolutionFor a planet revolving around sun, if a and b are the respective semi-major and semi-minor axes, then the square of its time period is proportional to
View SolutionA projectile is projected with a speed u at an angle θ with the horizontal. What is the speed when its direction of motion makes an angle θ/2 with the horizontal
View SolutionA heavy & big sphere is hang with a string of length l. This sphere move in a horizontal circular path making an angle θ with vertical then its time period is
View SolutionA simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
View Solution
