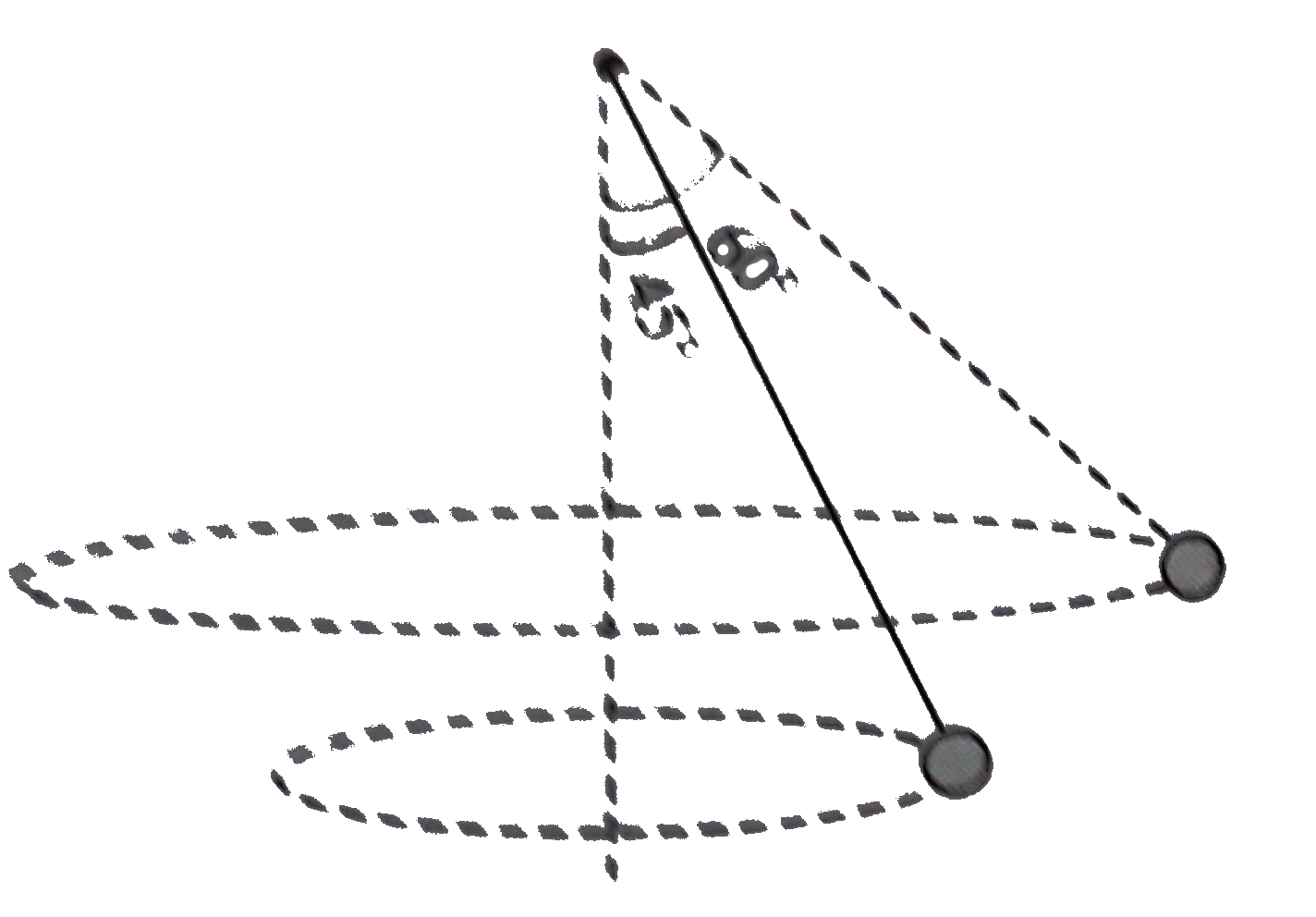
When the string of a conical pendulum makes an angle of 45∘ with the vertical , its time is T1 when the string makes an angle of 60∘ with the vertical , its time period is T2 then T21/T22is
2
√2
0.5
none of these
The correct Answer is:b
In conical pendulum
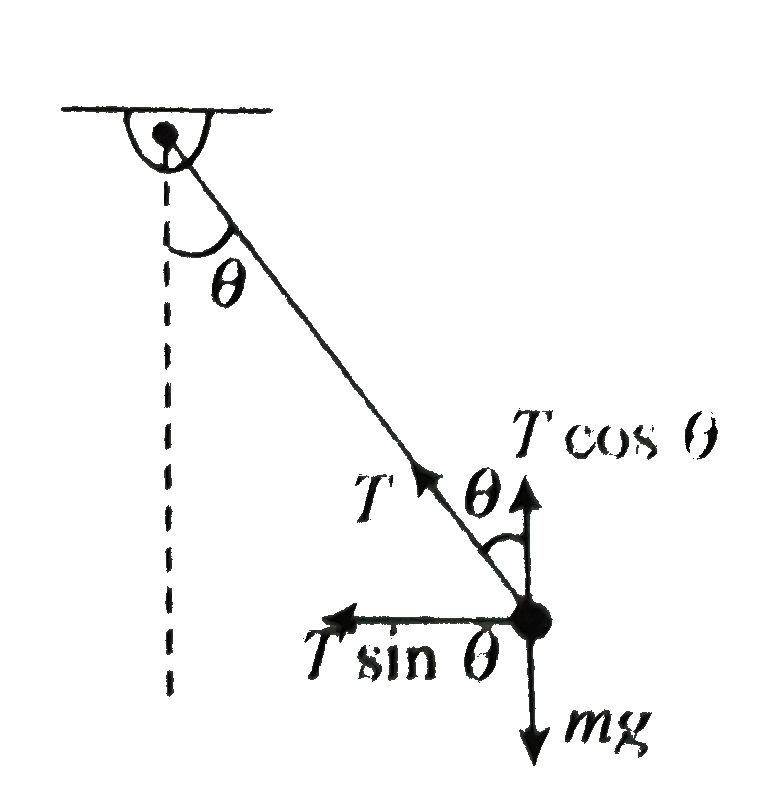
Tcosθ=mg= constant
T1cosθ1=T2cosθ2
T1T2=cosθ1cosθ2=cos60∘cos45∘
=1/21/√2=1√2
(T1T22)=12
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct2videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension52videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective21videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
A conical pendulum of length L makes an angle θ with the vertical. The time period will be
 A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√Lgtanθ
A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√Lgtanθ - Question 2 - Select One
A pendulum bob has a speed of 3ms−1 at its lowest position. The pendulum is 0.5 m long. The speed of the bob, when string makes an angle of 60∘ to the vertical is (take, g=10ms−1)
A2ms−1B12ms−1C1ms−1D2.5ms−1 - Question 3 - Select One
A simple pendulum has a time period T1 on the surface of earth of radius R. When taken to a height of R above the earth's surface, its time period is T2, ratio T2T is
A1√2B√2C2D4
The distance time graph of a particle at time t makes angle 45∘ with respect to time axis. After 1s, if makes angle 60∘ with respect to time axis. What is the acceleration of the particle?
View SolutionA stone of mass 2kg whirled in a horizontal circle attached at the end of 1.5 m long string. If the string makes an angle of 30∘ with vertical, compute its period (g=9.8m/s2) .
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.
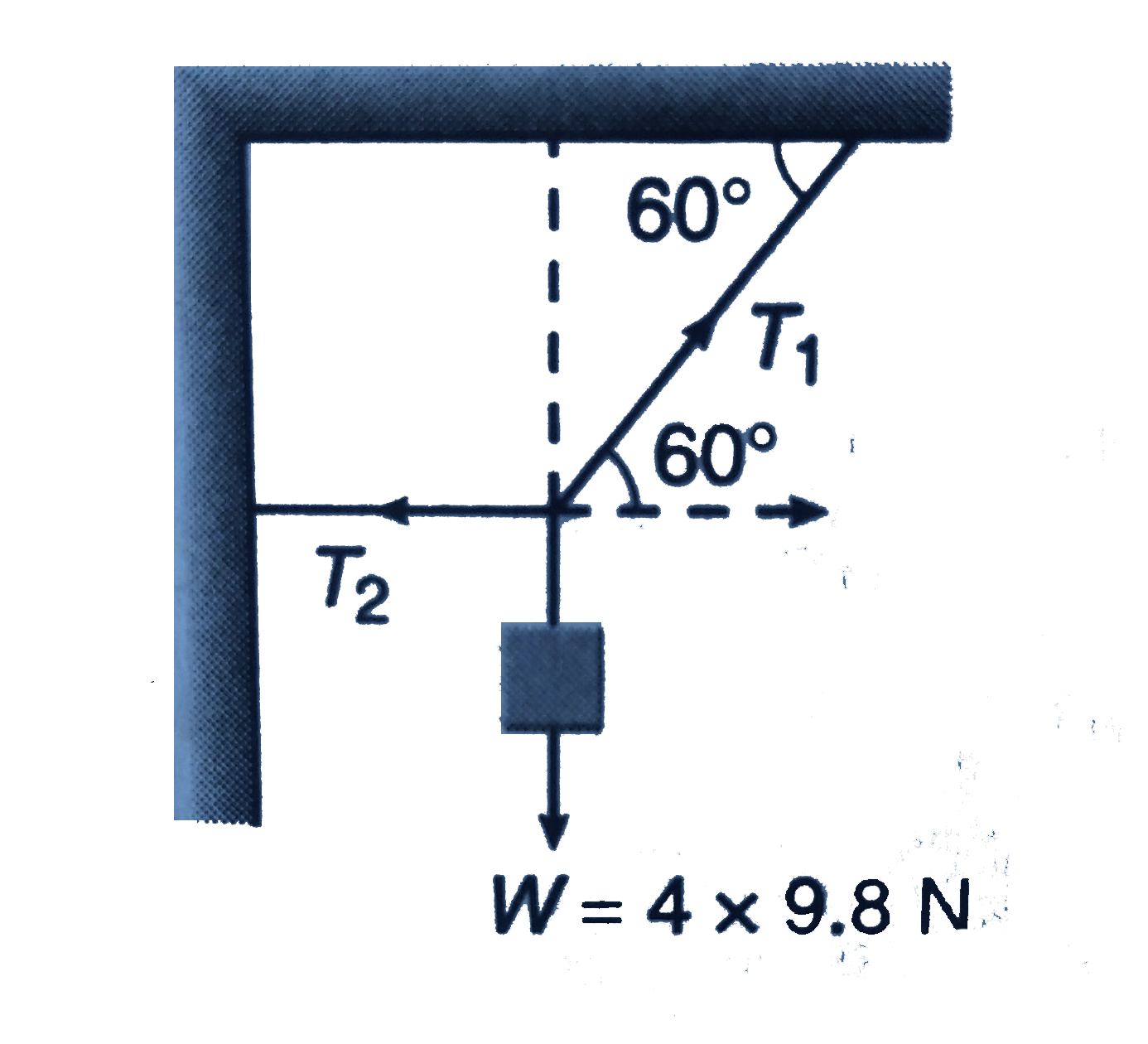 View Solution
View SolutionThe time period of a simple pendulum is T. When the length is increased by 10 cm, its period is T1. When the length is decreased by 10 cm, its period is T2. Then, the relation between T, T1 and T2 is
View SolutionTime period of a simple pendulum inside a lift that is accelerating up at 2ms−2 is T1. If left is retarding down at 6ms−2 then time period of same pendulum is T1. Then T1/T2 is
View Solution

