A square plate has a moment of inertia l0 about an axis lying in its plane, passing through its centre and making an angle θ with one of the sides. Which graph represents the variation of l with θ ?
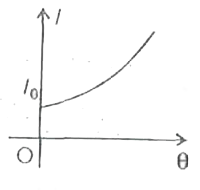
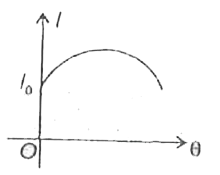
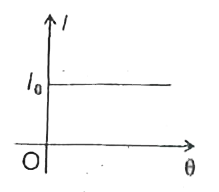

The correct Answer is:C
To solve the problem of the moment of inertia I of a square plate about an axis lying in its plane and making an angle θ with one of its sides, we can follow these steps:
Step 1: Understand the Moment of Inertia
The moment of inertia I of an object about an axis depends on the mass distribution relative to that axis. For a square plate, the moment of inertia about an axis through its center and parallel to one of its sides is given by:
I0=16ma2
where m is the mass of the plate and a is the length of one side of the square.
Step 2: Consider the Axis of Rotation
When the axis of rotation is tilted at an angle θ with respect to one of the sides, we need to consider how this affects the distribution of mass relative to the new axis. However, since the square plate is symmetric, the mass distribution does not change with the angle θ.
Step 3: Apply the Perpendicular Axis Theorem
For a flat plate, the perpendicular axis theorem states that the moment of inertia about an axis perpendicular to the plane of the plate is equal to the sum of the moments of inertia about two perpendicular axes in the plane of the plate. However, since we are rotating about an axis that is in the plane of the plate, we can conclude that the moment of inertia remains constant.
Step 4: Conclusion
Thus, the moment of inertia I about the tilted axis remains equal to I0 regardless of the angle θ. This means that the moment of inertia does not vary with θ.
Final Expression
I(θ)=I0
Graph Representation
The graph representing the variation of I with θ would be a horizontal line, indicating that I remains constant as θ changes.
---
The moment of inertia I of an object about an axis depends on the mass distribution relative to that axis. For a square plate, the moment of inertia about an axis through its center and parallel to one of its sides is given by:
When the axis of rotation is tilted at an angle θ with respect to one of the sides, we need to consider how this affects the distribution of mass relative to the new axis. However, since the square plate is symmetric, the mass distribution does not change with the angle θ.
For a flat plate, the perpendicular axis theorem states that the moment of inertia about an axis perpendicular to the plane of the plate is equal to the sum of the moments of inertia about two perpendicular axes in the plane of the plate. However, since we are rotating about an axis that is in the plane of the plate, we can conclude that the moment of inertia remains constant.
Thus, the moment of inertia I about the tilted axis remains equal to I0 regardless of the angle θ. This means that the moment of inertia does not vary with θ.
I(θ)=I0
The graph representing the variation of I with θ would be a horizontal line, indicating that I remains constant as θ changes.
Similar Questions
The moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View SolutionFind moment of inertia of a uniform rectangular plate (mass m) about axis AB lying in its plane and passing through center as shown in the figure.

View Solution
Knowledge Check
Find the moment of inortia of ring of mass m and radius R about an axis passing through its centre and making an angle of 45∘ with its plane:
 AMR24BMR22C34MR2DMR2
AMR24BMR22C34MR2DMR2Moment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
AI=12MR2BI=MR2CI=32MR2DI=52MR2The moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is
 Aml23sin2αBml212sin2αCml22cos2αDml22cos2α
Aml23sin2αBml212sin2αCml22cos2αDml22cos2α
Derive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionA uniform rectangular plate has moment of inertia about its longer side, equal to I. The moment of inertia of the plate about an axis in its plane, passing through the centre and parallel to the shorter sides is also equal to I. Find its moment of inertia about an axis passing through its centre and perpendicular to its plane.
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
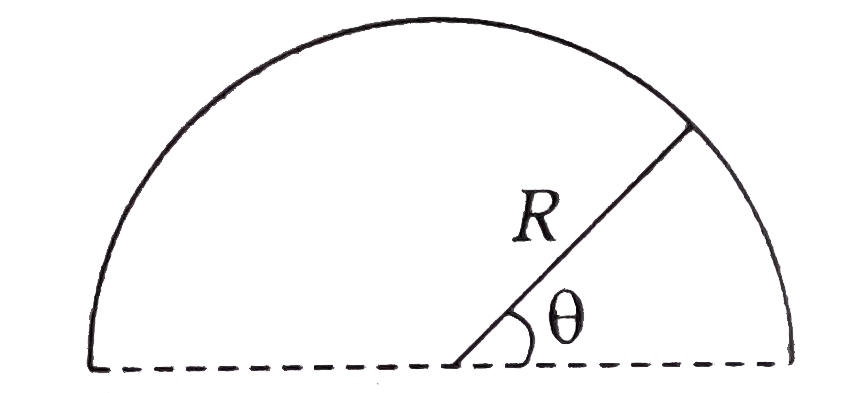
View SolutionThe moment of inertia of a semicircular ring of mass M and radius R about an axis which is passing through its centre and at an angle θ with the line joining its ends as shown in figure is
View Solution
