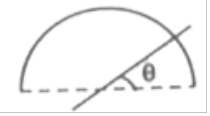
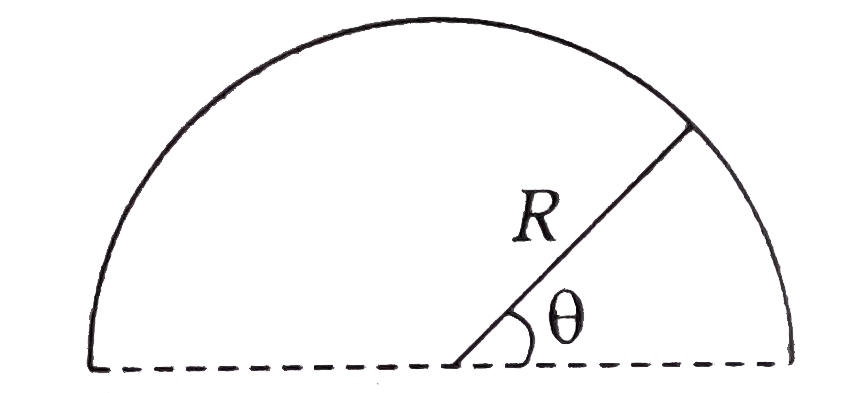
The moment of inertia of a semicircular ring of mass M and radius R about an axis which is passing through its centre and at an angle $θ$ with the line joining its ends as shown in figure is

A

$\frac{M R^{2}}{4} if θ = 0^{\circ}$

B

$\frac{M R^{2}}{2} if θ = 0^{\circ}$

C

$\frac{M R^{2}}{2} if θ =$ any angle

D

$\frac{M R^{2}}{2} if θ = 90^{\circ}$

Text Solution

Verified by Experts

The correct Answer is:C

If we complete the ring, its mass become 2m
. $∴ I_{whole ring} = \frac{1}{2} (2 M) (R^{2}) = M R^{2}$
$(I_{whole ring} = M I about any diameter)$
$∴ I_{Half ring} = \frac{1}{2} (M R^{2})$
This value is independent of angle $θ$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A $1 / 2 M R^{2}$
B $M R^{2}$
C $1 / 4 M R^{2}$
D $3 / 4 M R^{2}$
Question 2 - Select One
The moment of inertia of semicircular ring about its centre is
A $M R^{2}$
B $\frac{M R^{2}}{2}$
C $\frac{M R^{2}}{4}$
DNone of these
Question 3 - Select One
Find the moment of inortia of ring of mass m and radius R about an axis passing through its centre and making an angle of $45^{\circ}$ with its plane:

A $\frac{M R^{2}}{4}$
B $\frac{M R^{2}}{2}$
C $\frac{3}{4} M R^{2}$
D $M R^{2}$

DC PANDEY-ROTATION-(A) Chapter Exercises

Home
Ask Doubt
Profile