A force F is applied at the centre of a disc of mass M. The minimum value of coefficient of friction of the surface for rolling is
F2Mg
F3Mg
2F5Mg
2F7Mg
The correct Answer is:B
To solve the problem of finding the minimum value of the coefficient of friction (μ) for a disc of mass M rolling without slipping when a force F is applied at its center, we can follow these steps:
Step 1: Understand the Forces Acting on the Disc
- A force F is applied at the center of the disc.
- The frictional force f acts in the opposite direction to the applied force to prevent slipping.
- The disc has a mass M.
Step 2: Write the Equation of Motion
From Newton's second law, we can write the equation for the net force acting on the disc:
F−f=M⋅a(1)
where a is the linear acceleration of the center of mass of the disc.
Step 3: Relate Linear Acceleration to Angular Acceleration
For pure rolling motion, the acceleration a of the center of mass and the angular acceleration α are related by the equation:
a=α⋅r(2)
where r is the radius of the disc.
Step 4: Write the Torque Equation
The torque τ about the center of mass due to the frictional force is given by:
τ=f⋅r=I⋅α(3)
For a disc, the moment of inertia I is:
I=12Mr2
Substituting this into the torque equation gives:
f⋅r=12Mr2⋅α
Step 5: Substitute Angular Acceleration
Using equation (2), we can express α in terms of a:
f⋅r=12Mr2⋅ar
This simplifies to:
f=12Ma(4)
Step 6: Substitute Equation (4) into Equation (1)
Now we substitute equation (4) into equation (1):
F−12Ma=Ma
Rearranging gives:
F=Ma+12Ma=32Ma
Thus, we can solve for a:
a=2F3M(5)
Step 7: Find the Frictional Force
Substituting equation (5) back into equation (4) gives us the frictional force:
f=12M⋅2F3M=F3(6)
Step 8: Relate Frictional Force to Coefficient of Friction
The maximum static frictional force can be expressed as:
f=μ⋅N
where N=Mg is the normal force. Thus:
F3=μ⋅Mg
Step 9: Solve for the Coefficient of Friction
Rearranging gives:
μ=F3Mg
Final Answer
The minimum value of the coefficient of friction μ for rolling without slipping is:
μ=F3Mg
---
- A force F is applied at the center of the disc.
- The frictional force f acts in the opposite direction to the applied force to prevent slipping.
- The disc has a mass M.
From Newton's second law, we can write the equation for the net force acting on the disc:
F−f=M⋅a(1)
where a is the linear acceleration of the center of mass of the disc.
For pure rolling motion, the acceleration a of the center of mass and the angular acceleration α are related by the equation:
a=α⋅r(2)
where r is the radius of the disc.
The torque τ about the center of mass due to the frictional force is given by:
τ=f⋅r=I⋅α(3)
For a disc, the moment of inertia I is:
I=12Mr2
Substituting this into the torque equation gives:
f⋅r=12Mr2⋅α
Using equation (2), we can express α in terms of a:
f⋅r=12Mr2⋅ar
This simplifies to:
f=12Ma(4)
Now we substitute equation (4) into equation (1):
F−12Ma=Ma
Rearranging gives:
F=Ma+12Ma=32Ma
Thus, we can solve for a:
a=2F3M(5)
Substituting equation (5) back into equation (4) gives us the frictional force:
f=12M⋅2F3M=F3(6)
The maximum static frictional force can be expressed as:
f=μ⋅N
where N=Mg is the normal force. Thus:
F3=μ⋅Mg
Rearranging gives:
μ=F3Mg
The minimum value of the coefficient of friction μ for rolling without slipping is:
μ=F3Mg
Similar Questions
A horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation is μ find 100μ? (√3=1.74)
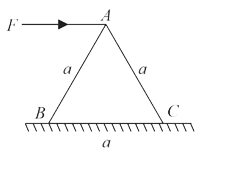
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force F is applied on the plank. What is the maximum value of F, if μ is coefficient of friction between sphere movment and plank and there is no slipping ?
View Solution
Knowledge Check
A horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation will be
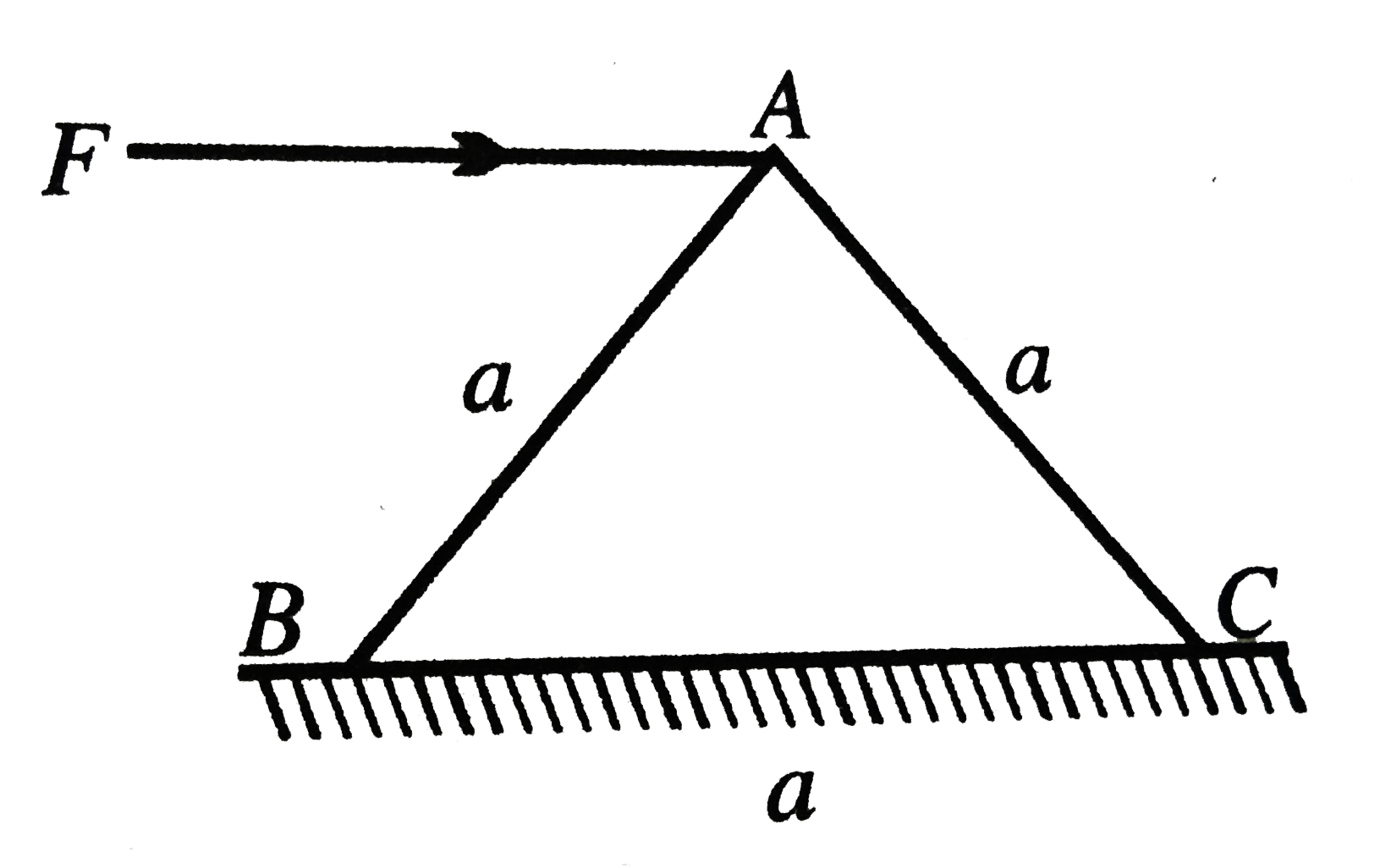 A2√3B13C1√3D12
A2√3B13C1√3D12A disc of mass M and radius R is placed on a rough horizontald surface. A light rod of length 2R is fixed to the disc at pointt A as shown in figure and force 32 Mg is applied at the other end of the rod. Find the minimum value of coefficient of friction (upto on decimal place ) between disc and horizontal surface, so that disc starts to roll without slipping .
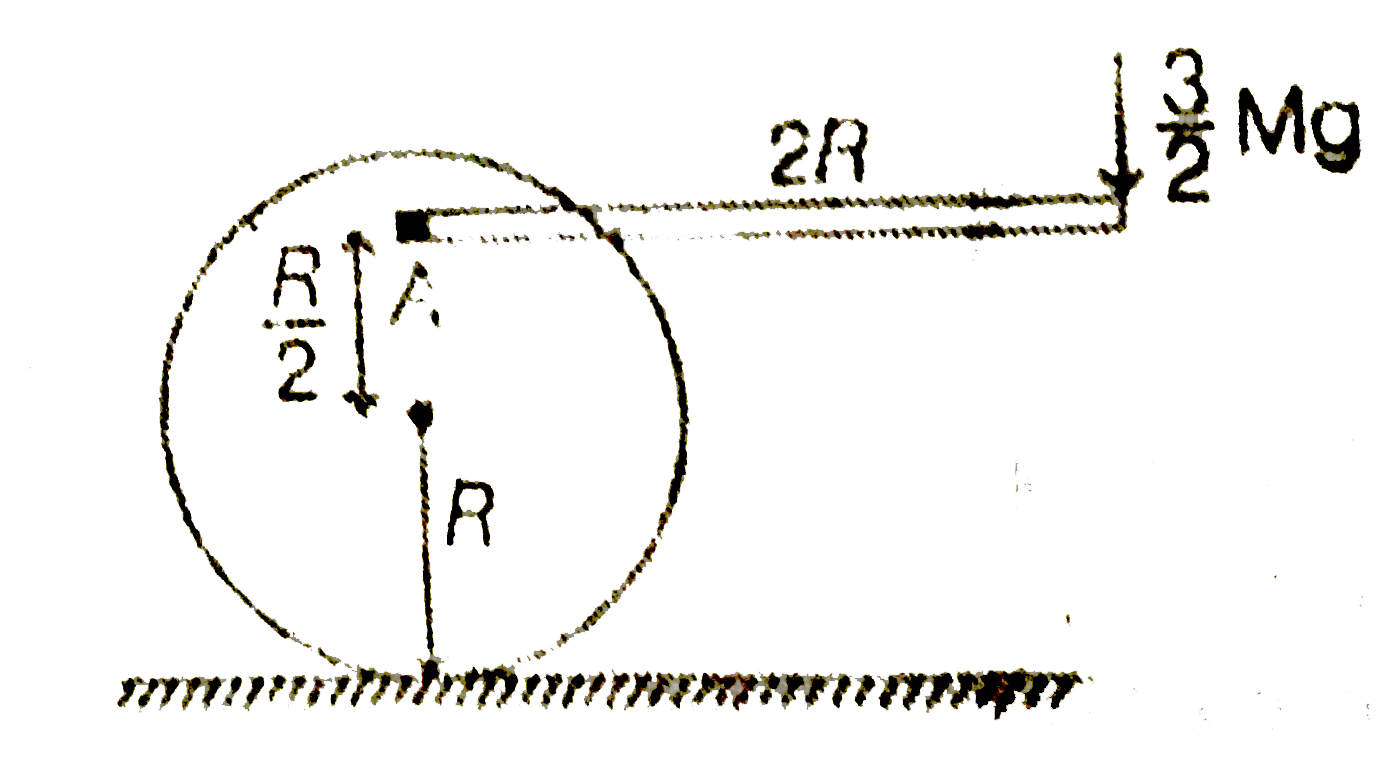 A0.2B0.4C0.6D0.8
A0.2B0.4C0.6D0.8A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 AF2 towards rightBF3 towards leftC2F3 towards rightDZero
AF2 towards rightBF3 towards leftC2F3 towards rightDZero
An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ . A horizontal force F is applied on the top of prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before topping, the minimum force required to topple the prism is

View SolutionA ring of mass M is kept on w horizontal rough surface . A force F is applied tangentially at its rim as shown . The coefficient of friction between the ring and surface is μ Then

View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.

View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is -
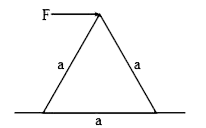
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
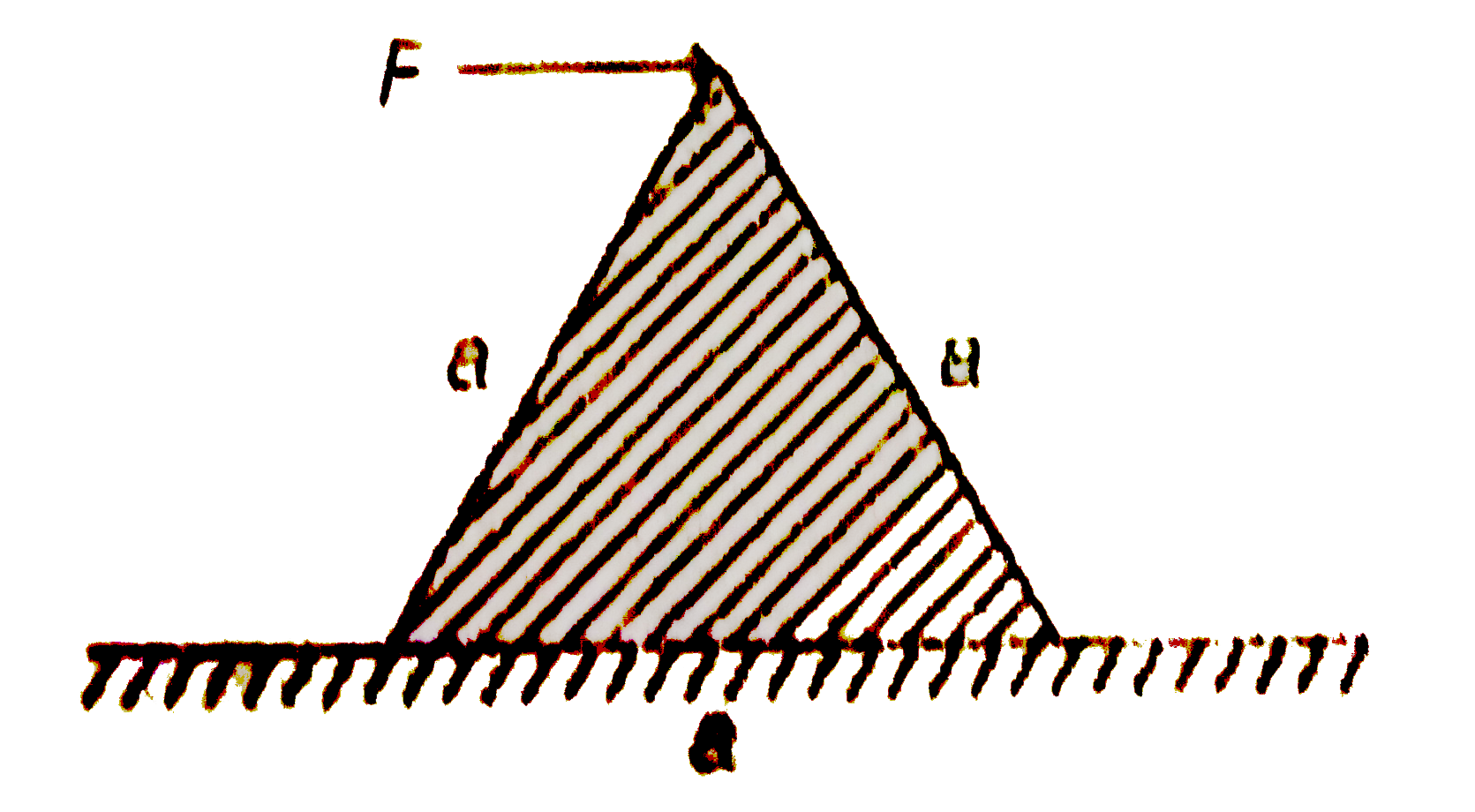
View Solution
