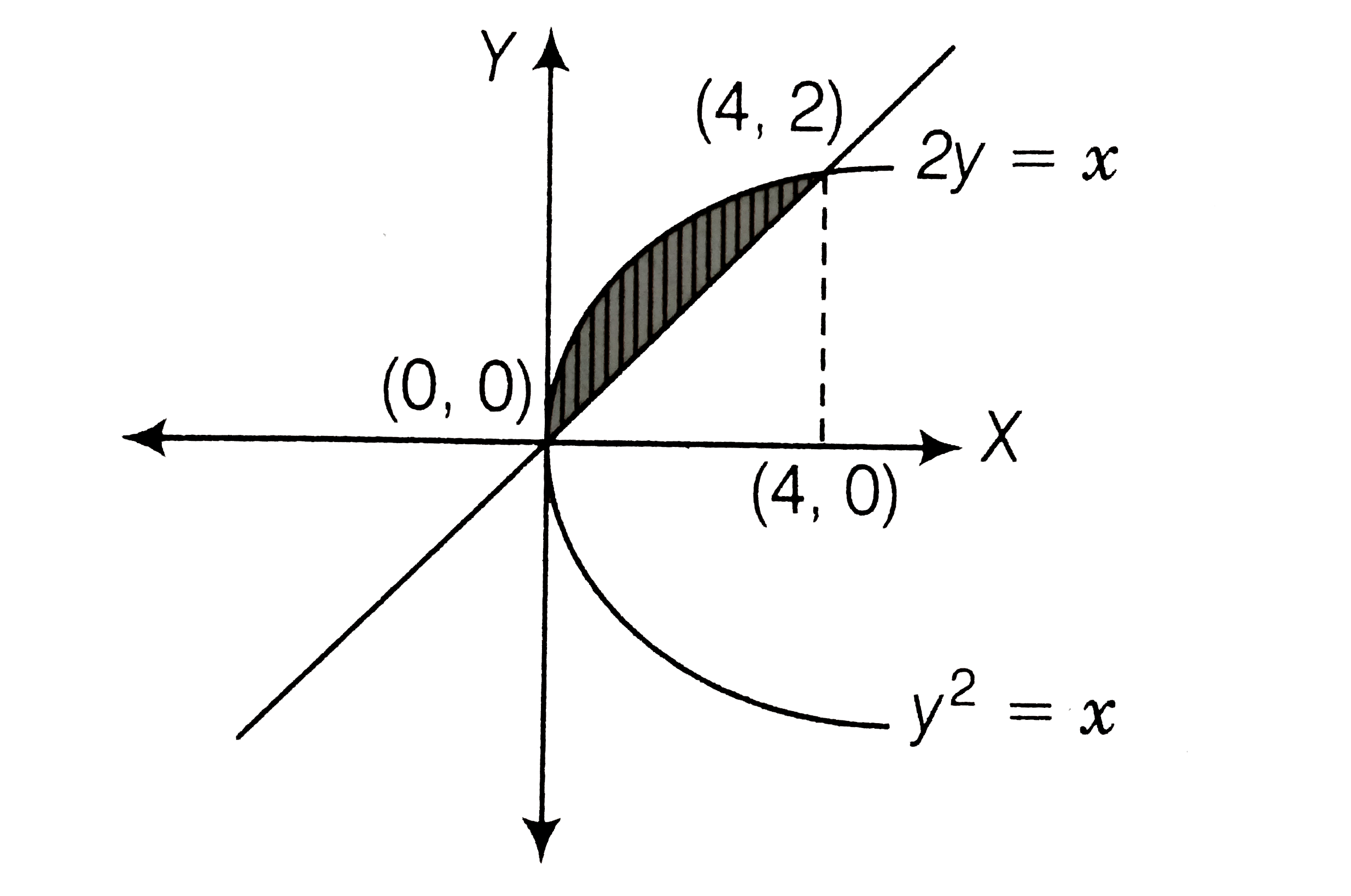
The area of the region bounded by parabola $y^{2} = x$ and the straight line $2 y = x$ is

$\frac{4}{3} sq units$

$1 sq unit$

$\frac{2}{3} sq unit$

$\frac{1}{3} sq units$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

The area of the region bounded by the parabola $y = x^{2} - 4 x + 5$ and the straight line $y = x + 1$ is
A $1 / 2$
B2
C3
D $9 / 2$
The area of the region bounded by the parabola $y^{2} = 9 x$ and the line $y = 3 x$ is :
A $\frac{1}{2}$ sq. units
B $\frac{1}{3}$ sq. units
C $\frac{1}{4}$ sq. units
D $\frac{2}{3}$ sq. units
The area of the region bounded by the parabola $y = x^{2}$ and the line y = 4x is
A $\frac{32}{3} s q . u n i t s$
B $\frac{16}{3} s q . u n i t s$
C $\frac{8}{3} s q . u n i t s$
D $\frac{4}{3} s q . u n i t s$