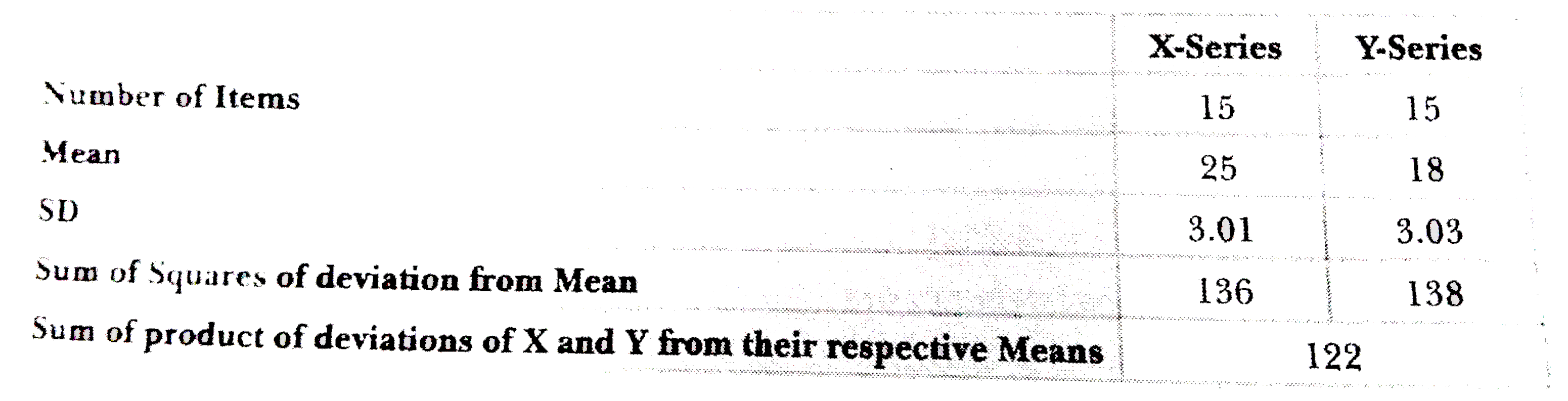
From the following data, compute the coefficient of correlation between X and Y series.
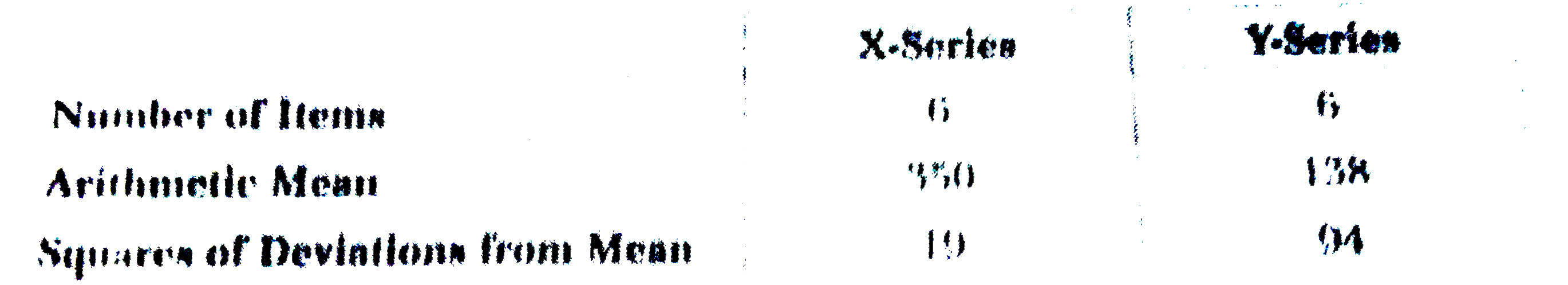
Summation of product of deviations of X and Y series from their respective arithmetic mean =41
We are given
N=6,¯¯¯X=350,¯¯¯Y=138,∑x2=19,∑y2=94,∑xy=41
r=∑xy√∑x2×∑y2
Substituting the values, we get
r=41√19×94=41√1,786=41√42.26=0.97
Coefficient of Correlation (r)=+0.97
Topper's Solved these Questions
- BOOK - TARUN JAIN & VK OHRICHAPTER - CORRELATIONEXERCISE - Learning by doing5videos
CORRELATION
- BOOK - TARUN JAIN & VK OHRICHAPTER - CORRELATIONEXERCISE - Objective type questions9videos
CORRELATION
- BOOK - TARUN JAIN & VK OHRICHAPTER - CONCEPT OF ECONOMICS AND SIGNIFICANCE OF STATISTICS IN ECONOMICSEXERCISE - NCERT Questions6videos
CONCEPT OF ECONOMICS AND SIGNIFICANCE OF STATISTICS IN ECONOMICS
- BOOK - TARUN JAIN & VK OHRICHAPTER - DIAGRAMMATIC PRESENTATION OF DATA BAR DIAGRAMS AND PIE DIAGRAMSEXERCISE - NCERT Question (With Hints to Answers)3videos
DIAGRAMMATIC PRESENTATION OF DATA BAR DIAGRAMS AND PIE DIAGRAMS
Similar Questions
Knowledge Check
- Question 1 - Select One
The sum of deviations of individual items of a series from arithmetic mean is
ALess than zeroBequal to zeroCMore than zeroDNone of these
From the following data, compute Karl Pearson coefficient of correlation :
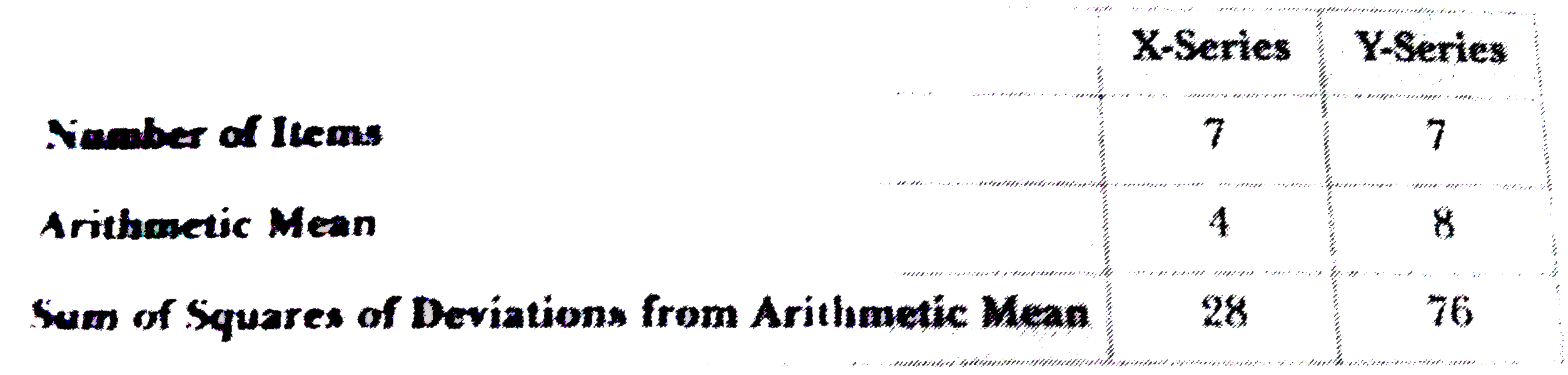
Summation of product of deviation of X and Y series from their respective means is 46View SolutionCalculate coefficient of correlation between series X and Y.
 View Solution
View SolutionFrom the following data, determine Karl Pearson's coefficient of correlation between X and Y series for 15 pairs .
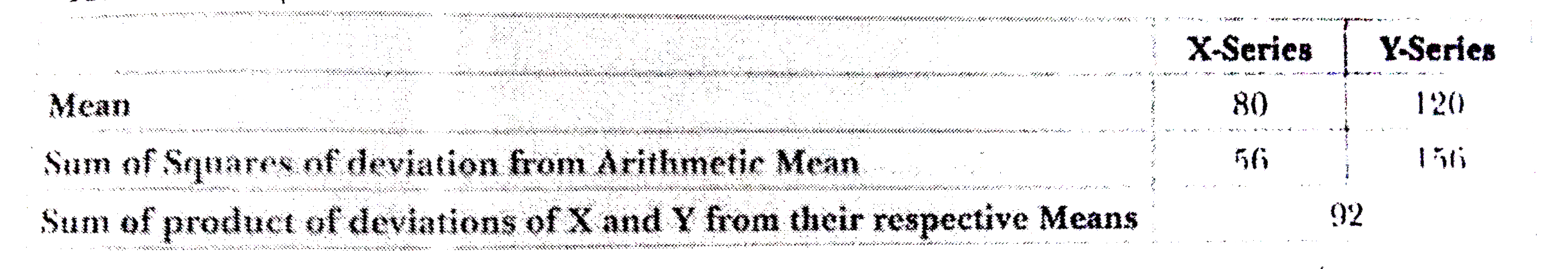 View Solution
View SolutionFind out Pearson's coefficient correlation between the following X and Y series using the deviation scores from their respective arithmetic mean. Interpret the results.
View SolutionFrom the following table, calculate the coefficient of correlation by Karl Pearson's method:

Arithmetic means of X and Y series are 6 and 8 respectively.View SolutionFind the Kari Pearson's Coefficient of correlation between x and y for the data
 View Solution
View SolutionFind the coefficient of correlation from the following data:
 View Solution
View Solution