The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
1λ=RH[122−1n2]n=3,4,5 . . .
RH=109678cm−1 is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
Q. Calculat ethe longest wavelength in Ã…(1Ã…=10−10m) in the balmer series of singly ionized helium He+. Select the correct answer. Ignore the nuclear motion in your calculation.
2651Ã…
1641.1Ã…
6569Ã…
3249Ã…
The correct Answer is:B
1λHe+=RHZ2[122−132]
=109678×4[536]
λHe+=1641.1Ã…
Topper's Solved these Questions
- ATOMIC STRUCTURE BOOK - OP TANDONCHAPTER - ATOMIC STRUCTURE EXERCISE - Self Assement
20 Videos
- ATOMIC STRUCTURE BOOK - OP TANDONCHAPTER - ATOMIC STRUCTURE EXERCISE - Integer Answer Type Questions
6 Videos
- ATOMIC STRUCTURE BOOK - OP TANDONCHAPTER - ATOMIC STRUCTURE EXERCISE - Integer Type Question
17 Videos
- AROMATIC HYDROCARBONS (ARENES)BOOK - OP TANDONCHAPTER - AROMATIC HYDROCARBONS (ARENES)EXERCISE - EXAMPLES
24 Videos
- CHARACTERISATION OF ORGANIC COMPOUNDS BOOK - OP TANDONCHAPTER - CHARACTERISATION OF ORGANIC COMPOUNDS EXERCISE - Passage-2
5 Videos
Similar Questions
Hydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Calculate the iongest wavelength in A(1Å=10−10m) in the 'Balmer series of singly ionized helium (He+) Ignore nuclear motion in your calculation.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
H− is a two-electron atomic system. Assuming that the Bohr energy formula is valid for each electron with nuclear charge Z replaced by Zeff' calculate Zeff for H−.
View Solution
Knowledge Check
The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
1λ=RH[122−1n2]n=3,4,5 . . .
RH=109678cm−1 is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
Which of the following is not correctly matched?AHα−6569Ã…(Red)BHβ−4861Ã…CHγ−4340Ã… (Orange)DHδ−4101Ã…(Violet)The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
1λ=RH[122−1n2]n=3,4,5 . . .
RH=109678cm−1 is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
The wavelength of first line of Balmer spectrum of hydrogen will be:A4340Ã…B4101Ã…C6569Ã…D4861Ã…The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
1λ=RH[122−1n2]n=3,4,5 . . .
RH=109678cm−1 is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
Q.In which region of electromagnetic spectrum does the Balmer series lie?AUVBVisibleCInfraredDFar infrared
Hydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Determine the loest energy and the radius of the Bohr orbit of the muonic hydrogen atom. Ignore the motion of the nucleus in your calculation. The radius of the Bohr orbit of a hydrogen atom
(called the Bohr radius,a0=ε0h2mee2∏is0.53Å)
The classical picture of an ''orbit'' in Bohr's theory has now been replaced by the quantum mechanical nation of an 'orbital'. The orbital ψ1σ1s(r) for the ground state of a hydrogen atom is given by
ψ1s(r)=1√∏a30era0
where r is the distance of the electron from the nucleus and a0 is the Bohr radius.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Determine the values of the dissociation energies (DeineV) of the H2 molecule corresponding to channel (i)
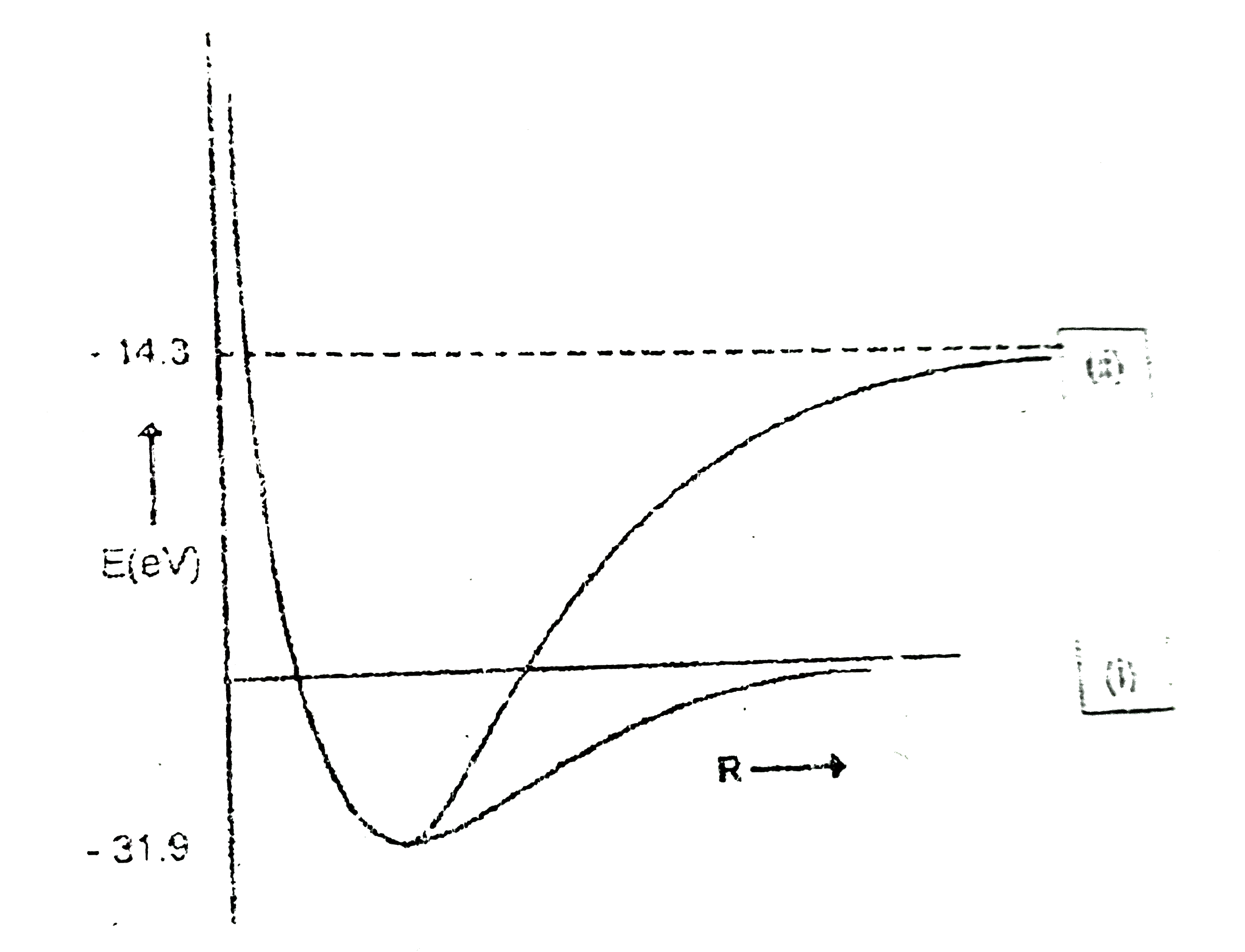View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
A formula analogous to Balmer's formula applies to the series of spectral lines which arise from transition from higher energy levels to the lowest energy level of hydrogen atom. Write this formula and use it to determine the ground state energy of a hydrogen atom in eV.
A 'muonic hydrogen atom' is like a hydrogen atom in which the electron is replaced by a heavier particle, the muon. The mass of a muon is about 207 times the mass of an electron, while its charge is the same as that of an electron. A muon has a very short lifetime, but we ignore its ubstable nature here.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
From the given data, calculate the energy change for the process
H−→H+e−
View SolutionThe observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
1λ=RH[122−1n2]n=3,4,5 . . .
RH=109678cm−1 is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.Howmany lines in the spectrum will be observed when electrons return from 7th shell to 2nd shell?
View Solution