A running track of 440 ft is to be laid out enclosing a football field, the shape of which is a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum, then find the length of its sides.
Step by step video & image solution for A running track of 440 ft is to be laid out enclosing a football field, the shape of which is a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum, then find the length of its sides. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A running track of 440 ft is to be laid out enclosing a football field, the shape of which is a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum, then find the length of its sides.
View SolutionA field has the shape of a rectangle having a semi-circle at its one end as shown in the figure. Find the area of the field.
View Solution
Knowledge Check
A playground is in the form of a rectangle having semicircle on the shorter sides. Find its area when the length of the rectangular portion is 80 m and the breadth is 42 m.
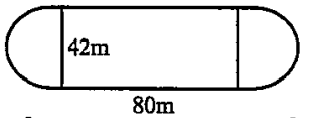 A4746m2B4748m2C4950m2D5049m2
A4746m2B4748m2C4950m2D5049m2Find the radius of the semic-circle.
I. The area of semi-circle is equal to the area of the rectangle.
II. The breadth of rectangle is 5 cm less than its length and its permeter is 50 cm.Aif the data in statement I alone are sufficient to answer the questin, while the data in statement II alone are not sufficient to answer the question.Bif the data in statement II alon are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question.Cif the data either in statement I alone or in statement II alone in sufficient to answer the question.Dif the data in both the statements I and II together are necessary to answer the question.From four corners of a square sheet of side 4 cm, four pieces, each in the shape of arc of a circle with radius 2 cm, are cut out. The area of the remaining portion is :
A(8−π) sq. mB(16−4π) sq. cmC(16−8π) sq. cmD(4−2π) sq. cm.
A window is in the shape of a rectangle surmounted by a semi circle. If the perimeter of the window is of fixed length then the maximum area of the window is
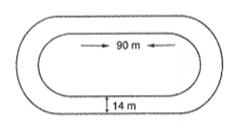
View SolutionThe inside perimeter of a running track (shown in figure) is 400m. The length of each of the straight portion is 90m and the ends are semi-circles. If the track is everywhere 14m wide, find the area of the track. Also find the length of the outer running track.
View SolutionThe inside perimeter of a running track (shown in figure) is 400m. The length of each of the straight portion is 90m and the ends are semi-circles. If track is everywhere 14m wide, find the area of the track. Also, find the length of the outer running track.
View SolutionA playground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36m and 24.5m, find the area of the playground. (Take π=227)
View SolutionThe inner perimeter of a running track (shown in figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semicircular. If the track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.

View Solution