Two batteries of emf e1ande2 having internal resistance r1andr2 respectively are connected in series to an external resistance R. Both the batteries are getting discharged. The above described combination of these two batteries has to produce a weaker current than when any one of the batteries is connected to the same resistor. For this requirement to be fulfilled
ε2ε1must not lie betweenr2r1+Randr1r2+R
ε2ε1must not lie betweenr2r1+Randr2+Rr1
ε2ε1must lie betweenr2r1+Randr1r2+R
ε2ε1must not lie betweenr2r1+Randr2+Rr1
The correct Answer is:B
Let R' be the resistance of the heater of coil.
R'=V2P=(100)21000>10Ω
If the heater has to operature with a power P'=62.5W, the voltage V' across its coil should be
V'=(P'R')1/2=(6.25×10)1/2=25VA
Thus, out of 100V, a valtage drop of 25V occurs across the heater and the rest 100-25=75V occurs across the 10Ω resistor. Therefore current in the cicruit is I=7510=7.5A
Now, current throght the heater =V'R=2510=2.5A
Therefore, current throgh reistor R=7.5-2.5=5.0A
Here,R=V'5.0A=25V5.0=5Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT FINGERTIPSChapter:CURRENT ELECTRICITYExercise:NCERT Exemplar
Explore 6 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTIPSChapter:CURRENT ELECTRICITYExercise:Assertion And Reason
Explore 15 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTIPSChapter:CURRENT ELECTRICITYExercise:Potentiometer
Explore 7 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTIPSChapter:COMMUNITCATION SYSTEMSExercise:HOTS
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTIPSChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Two batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
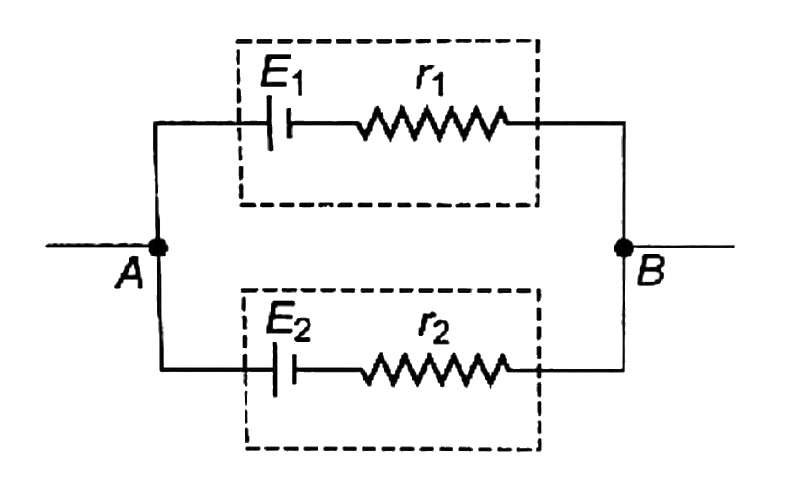
View Solution
Knowledge Check
Two batteris of emf ε1 and ε2 wit respective internal resistance r1 and r2 are connected in parallel. Now
AThe effective emf of this parallel combination is (ε1r1+ε2r2)(r1+r2)BThe effective internal resistance of this combination is 2r1r2(r1+r2)Cthe effective emf of this parallel combination is (ε1r2+ε2r1)(r1+r2)DThe effective internal resistance of this combination is r1r2(r1+r2)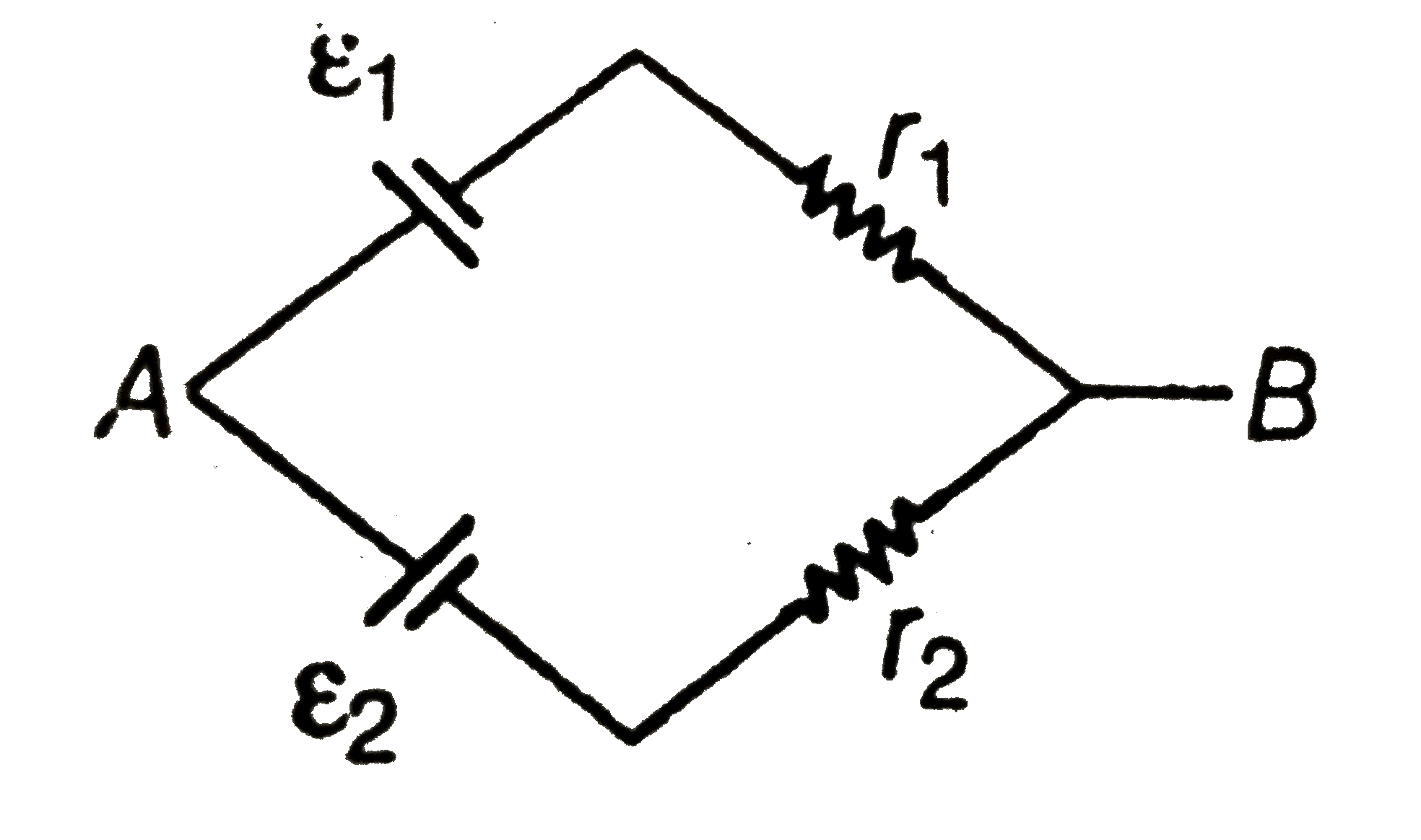
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.AThe equivalent emf εeq of the two cells is between ε1andε2, i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 always.Dεeq is independent of internal resistance r1andr2.Two batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.
 AThe equivalent emf εeq of the two cells is between ε1 and ε2,i.e.,ε1<εeq<ε2BThe quivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 alwaysDεeq is independent of internal resistances r1 and r2
AThe equivalent emf εeq of the two cells is between ε1 and ε2,i.e.,ε1<εeq<ε2BThe quivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 alwaysDεeq is independent of internal resistances r1 and r2
Two ideal batteries of emf V1andV2 and these resistances R1,R2andR3 are connected as shown in the figure . The current in resistance R2 would be zero if
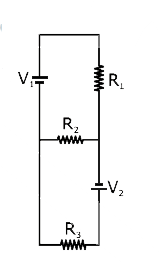
View SolutionTwo ideal batteries of emfV1andV2 and three resistance R1R2andR3 are connected The current in resistance R2 would be zero if
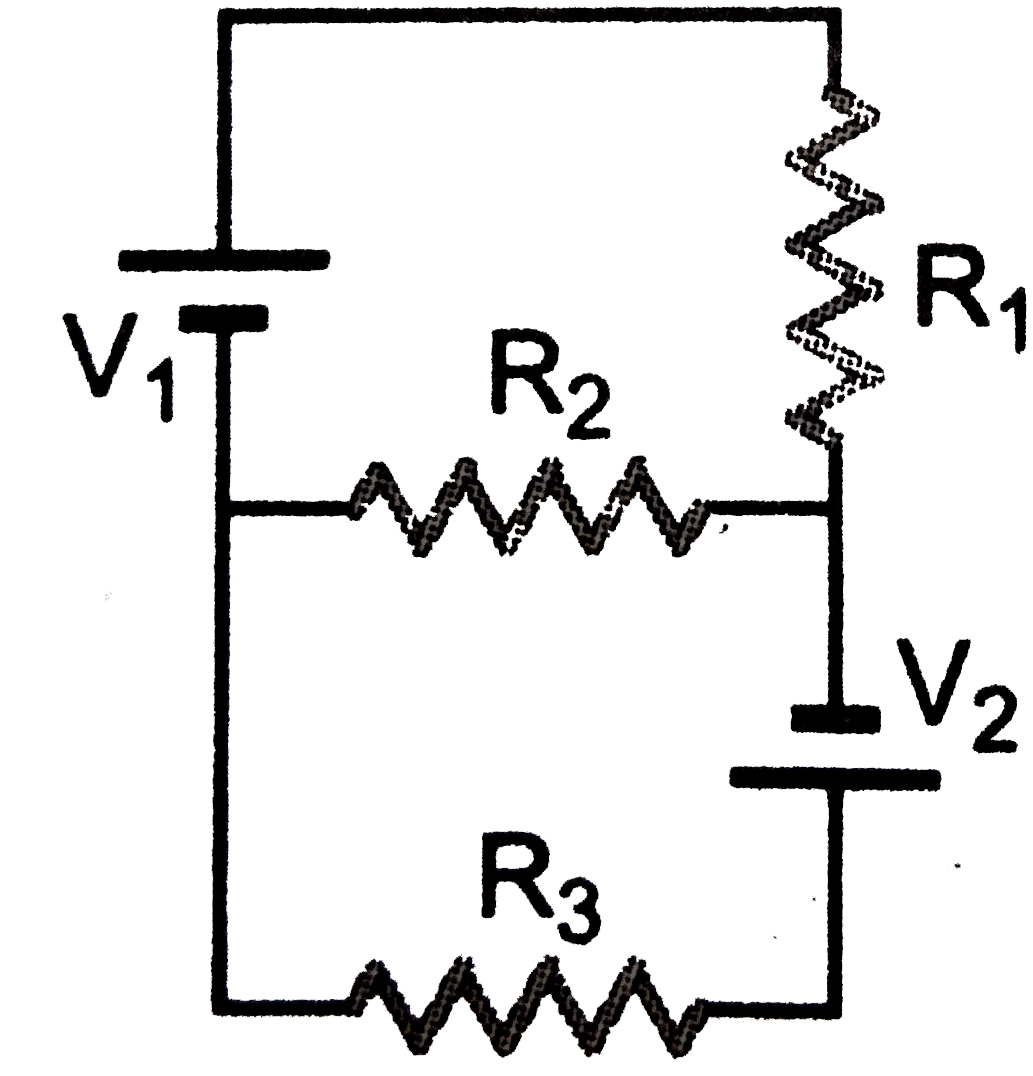
View SolutionThree batteries of emf E1,E2 and E3 and internal resistance r1,r2 and r3 are connected as shown. The current through the battery of emf E3 is zero if.
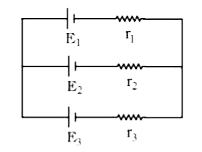
View SolutionTwo batteries of emfs 2 V and 1 V of internal resistances 1Ωand2Ω respectively are connected in parallel. The effective emf of the combination is
View SolutionN batteries each of emf E and internal resistance r are first connected in series and then in parallel to an external resistance R. if current through R is same in both cases then.
View Solution