Three batteries of emf E1,E2 and E3 and internal resistance r1,r2 and r3 are connected as shown. The current through the battery of emf E3 is zero if.
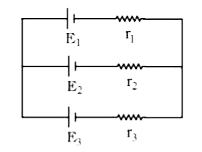
E1r2+E2r1=E3(r1+r2)
E1r2−E2r1=E3(r1+r2)
E1r2+E2r1=E3(r1+r2)
E1r1+E2r2=E3(r1+r2)
The correct Answer is:A
Let us assume that E1>E2
Current through the loop containing the batteries of emf E1andE2
i=E1−E2r1+r2 (anti-clockwise)
Now, equating potential difference across the ends of the battery of emf E3
ir2+E2=E3⇒(E1−E2r1+r2)r2+E2=E3⇒E1r2+E2r1=E3(r1+r2)
Similar Questions
Knowledge Check
Two ideal batteries of emfV1andV2 and three resistance R1R2andR3 are connected The current in resistance R2 would be zero if
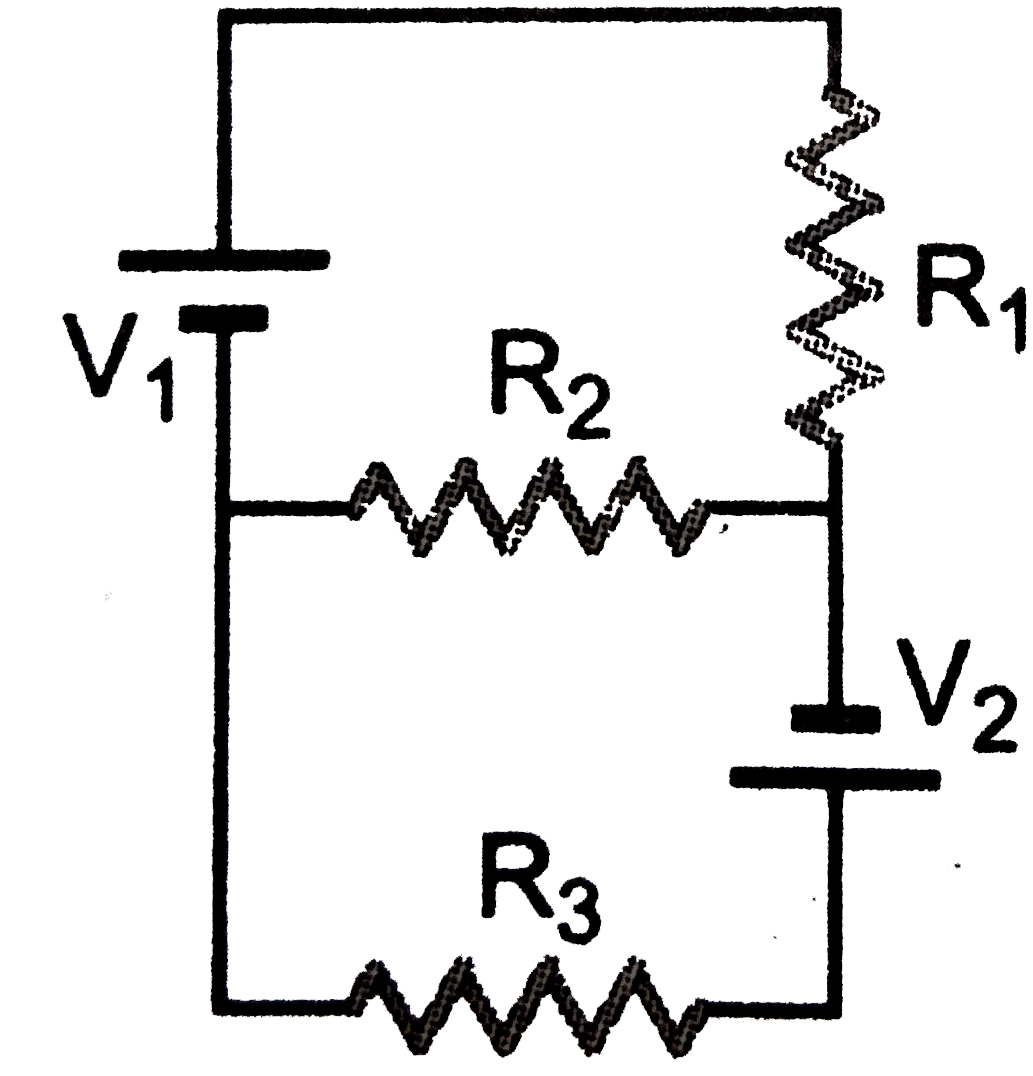 AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and2R1=R2=R3
AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and2R1=R2=R3Two ideal batteries of emf V1andV2 and three resistances R1,R2andR3 are connected as shown in the figure. The current in resistance R2 would be zero if
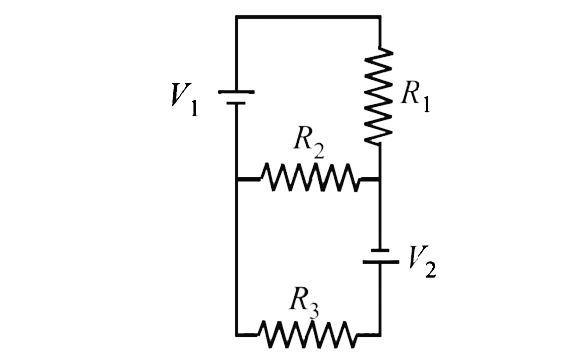 AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and3R1=R2=R3
AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and3R1=R2=R3
Two ideal batteries of emfV1andV2 and three resistance R1R2andR3 are connected The current in resistance R2 would be zero if
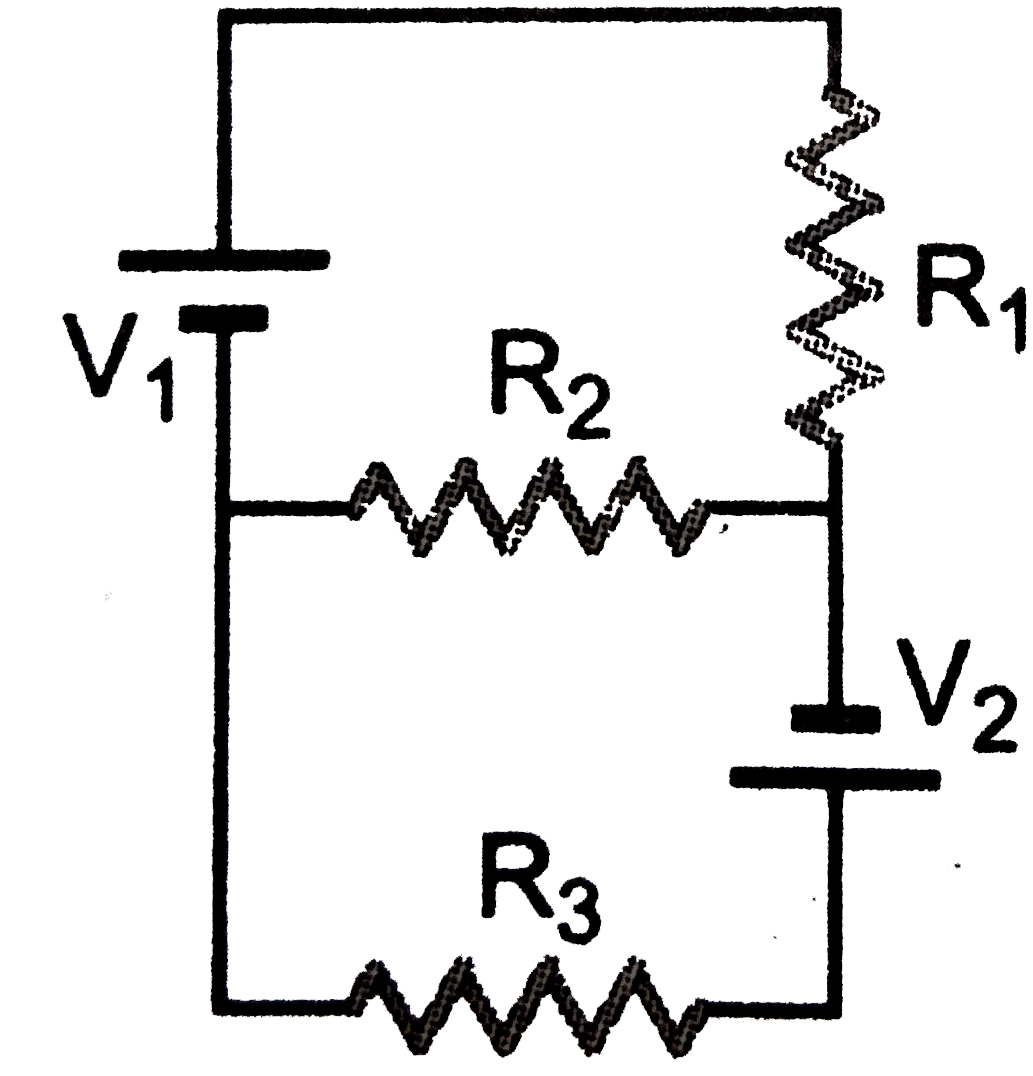
View SolutionTwo batteries of emf E1andE2(E2>E1) and internal resistances r1andr2 respectively are connected in parallel as shown in figure.

View SolutionTwo ideal batteries of emf V1andV2 and three resistances R1,R2andR3 are connected as shown in the figure. The current in resistance R2 would be zero if

View SolutionTwo ideal batteries of emf V1andV2 and these resistances R1,R2andR3 are connected as shown in the figure . The current in resistance R2 would be zero if
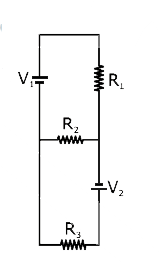
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
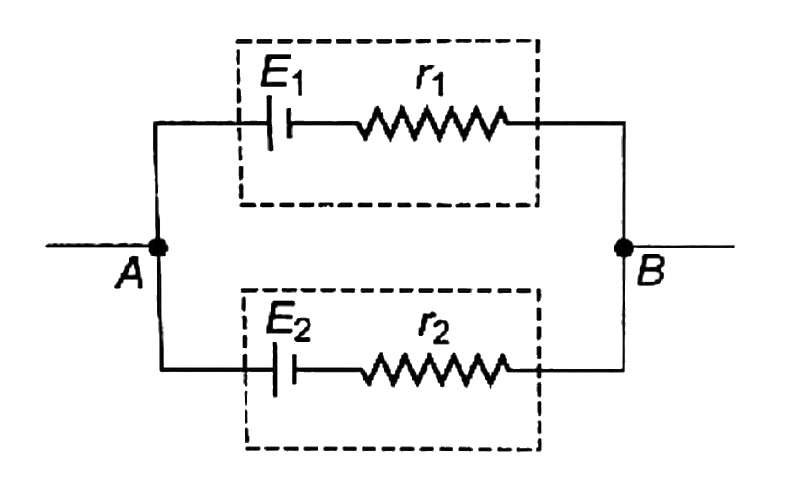
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?

View Solution
