In a rectangle ABCD, diagonals AC and BD intersect at O. If ∠OAB=35∘, find :
(a)∠ABC(b)∠ABO(c)∠CO(d)∠BOC)
Video Solution
Text Solution
(a) In∠ABC,∠ABC=90∘
∴∠ACB=180∘−∠ABC−∠CAB
180∘−90∘−35∘=55∘
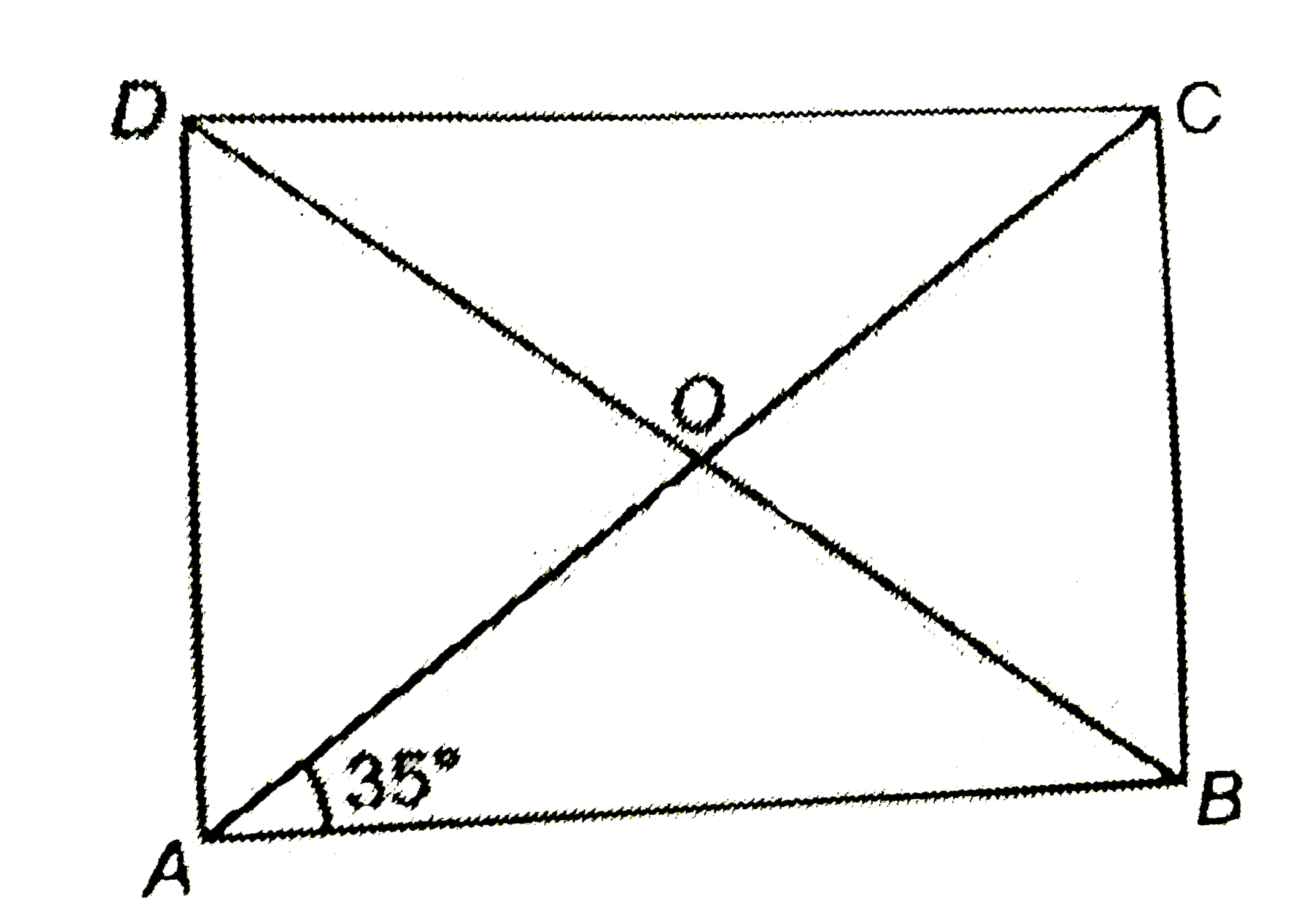
(b) InΔABO,OA=OB
∴ ∠ABO=∠OAB=35∘
( c) ∠COD=∠AOB
=180∘−∠OAB−∠OBA
=180∘−35∘−35∘
=110∘
(d) ∠BOC+∠COD=180∘
∴ ∠BOC=180∘−∠COD=180∘−110∘=70∘
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise10videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, ABCD is a rectangle whose diagonals AC and BD intersect at 0. If ∠OAB=28∘, then ∠OBC is equal to
 A72∘B50∘C62∘D75∘
A72∘B50∘C62∘D75∘
The diagonals of a rectangle ABCD intersect in O. if angleBOC=68∘, find angle ODA
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=50∘ then find ∠ODA.
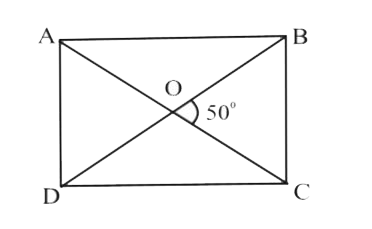 View Solution
View SolutionIn the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
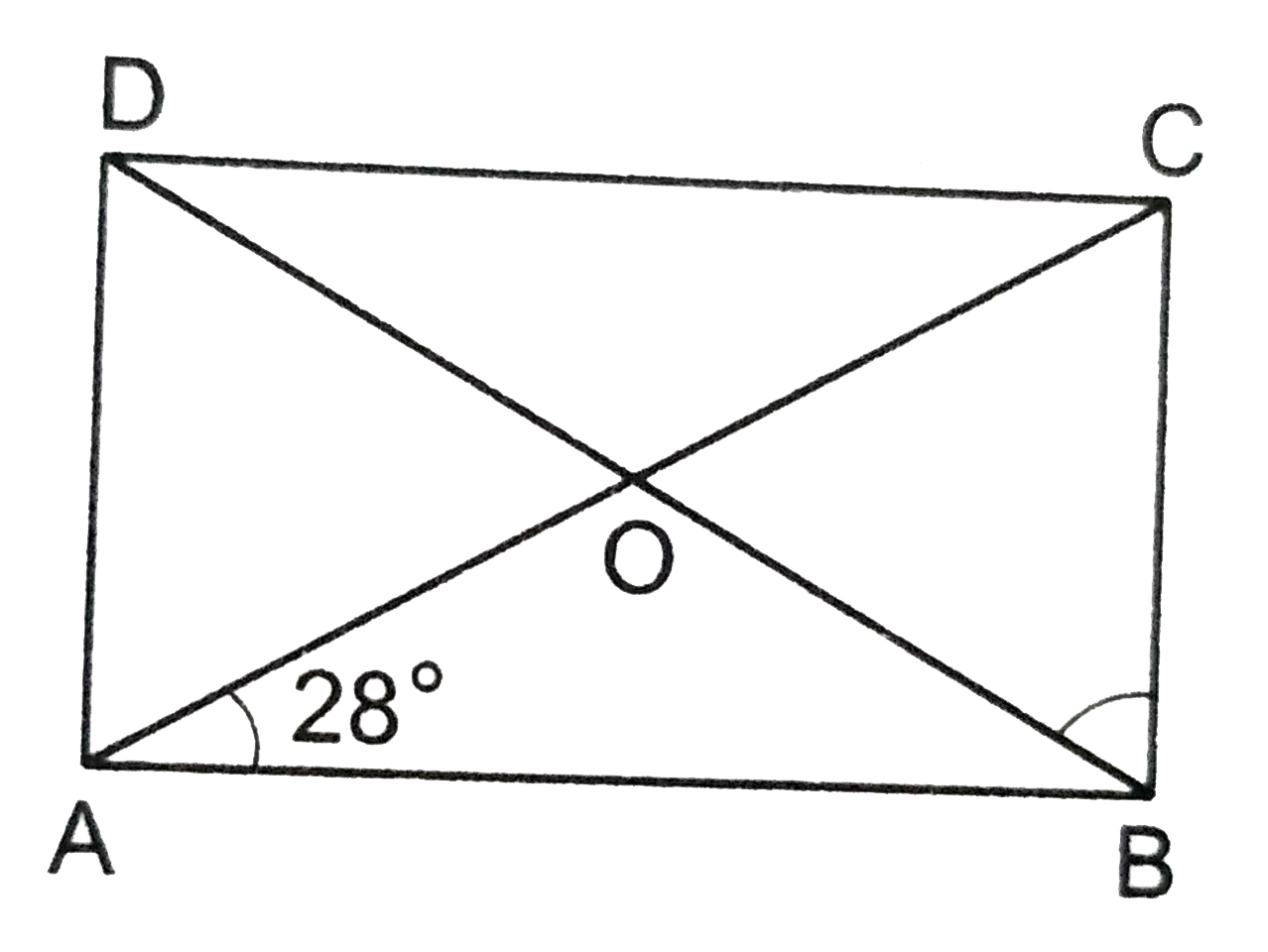 View Solution
View SolutionThe diagonals of a rectangle ABCD intersect in O. If ∠BOC=680, find ∠ODA.
View SolutionIn a rectangle ABCD, diagonal AC and BD intersect each other at 0.If AB=32 cm and AD = 24 cm, find the length of OD.
View SolutionThe diagonals of a rectangle ABCD intersects at O. If ∠BOC=70∘. find ∠ODA.
View SolutionIf ABCD is a quadrilateral whose diagonals AC and BD intersect at O, then
 View Solution
View Solution


