In a rectangle ABCD, diagonal AC and BD intersect each other at 0.If AB=32 cm and AD = 24 cm, find the length of OD.
40 cm
60 cm
80 cm
20 cm
To solve the problem, we need to find the length of OD in rectangle ABCD, where diagonals AC and BD intersect at point O. Given that AB = 32 cm and AD = 24 cm, we can use the properties of rectangles and the Pythagorean theorem to find the solution.
1. Identify the sides of the rectangle:
- AB = 32 cm (length)
- AD = 24 cm (width)
2. Use the Pythagorean theorem to find the length of diagonal BD:
- In triangle ABD, we can apply the Pythagorean theorem:
BD2=AB2+AD2
- Substitute the values:
BD2=322+242
3. Calculate the squares:
- Calculate 322:
322=1024
- Calculate 242:
242=576
4. Add the squares:
- Now add the two results:
BD2=1024+576=1600
5. Take the square root to find BD:
- Find BD by taking the square root:
BD=√1600=40 cm
6. Use the property of diagonals in a rectangle:
- The diagonals of a rectangle bisect each other, which means:
BO=OD=BD2
7. Calculate OD:
- Substitute the value of BD:
OD=402=20 cm
Final Answer:
The length of OD is 20 cm.
---
- AB = 32 cm (length)
- AD = 24 cm (width)
- In triangle ABD, we can apply the Pythagorean theorem:
BD2=AB2+AD2
- Substitute the values:
BD2=322+242
- Calculate 322:
322=1024
- Calculate 242:
242=576
- Now add the two results:
BD2=1024+576=1600
- Find BD by taking the square root:
BD=√1600=40 cm
- The diagonals of a rectangle bisect each other, which means:
BO=OD=BD2
- Substitute the value of BD:
OD=402=20 cm
The length of OD is 20 cm.
Similar Questions
Knowledge Check
In a trapezium ABCD, the diagonals AC and BD interserted other at O such that OB:OD=3:1 then the ratio of area of ΔAOB:ΔCOD is :
A3:1B1:4C9:1Dcan't be determinedDiagonals AC and BD of a parallelogram ABCD intersect at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
AAC=6cm,BD=2cmBAC=6cm,BD=4cmCAC=3cm,BD=4cmDAC=3cm,BD=3cm
In a parallelogram ABCD diagonals AC and BD intersect at O and AC =12.6 cm and BD = 9.4 cm. Find the measures of OC and OD.
View SolutionDiagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA= 3 cm and OD = 2 cm, determine the lengths of AC and BD.
View SolutionIn rhombus ABCD, diagonals AC and BD intersect each other at point O If cosine of angle CAB is 0.6 and OB 8 cm, find the lengths of the side and the diagonals of the rhombus.
View SolutionIn the adjacent figure , ABCD is a rhombus whose diagonals AC and BD intersect at a point O. If side AB=10 cm and diagonal BD=16 cm , find the length of diagonal AC.
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8cm and BD=13.6cm. Find the measures of OC and OD.
View SolutionIn the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
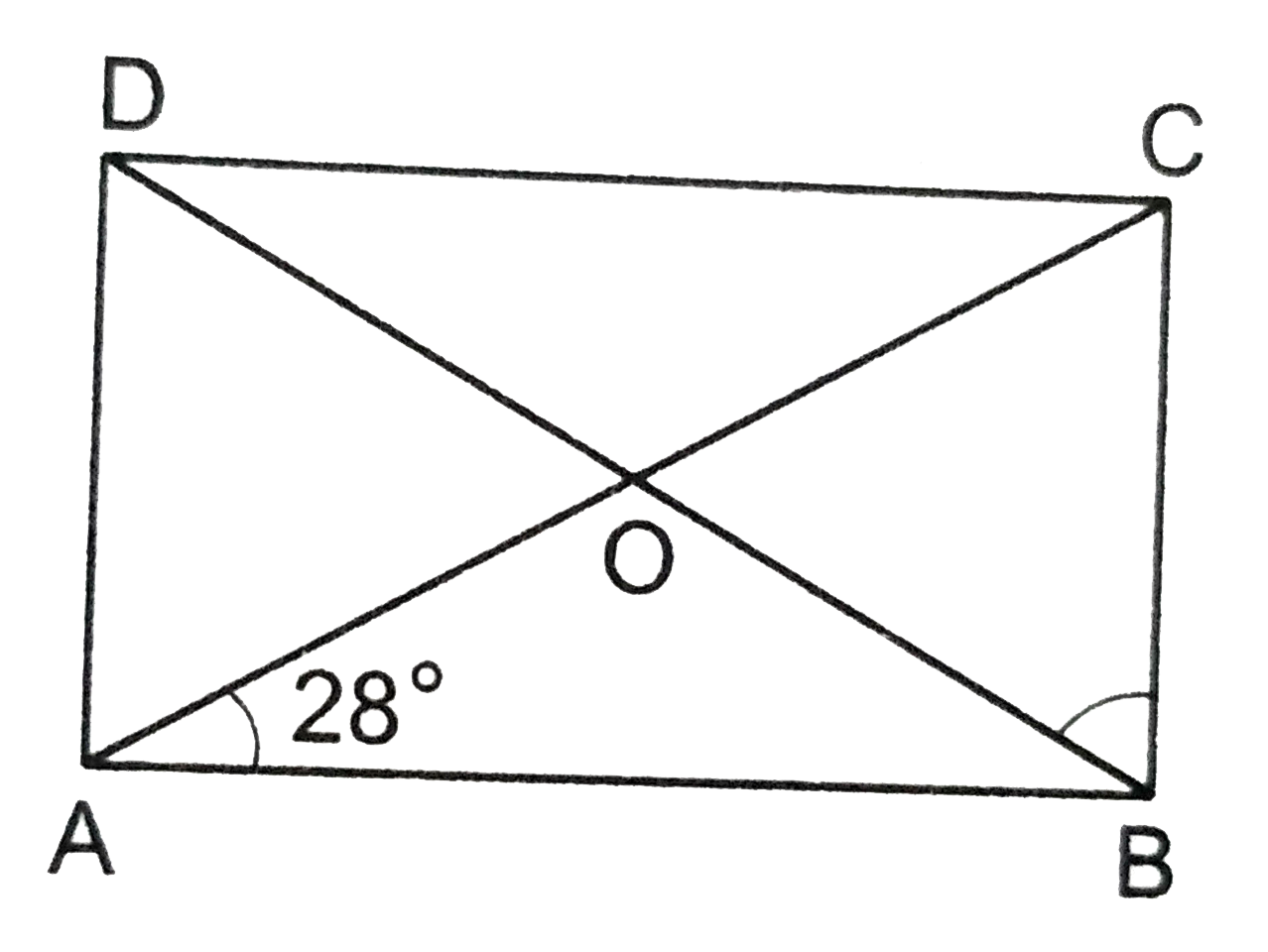
View Solution
