In quadrilateral ABCD, AB ||CD and AD= BC, prove that ∠A=∠B.
To prove that in quadrilateral ABCD, where AB is parallel to CD and AD = BC, we have angle A = angle B, we can follow these steps:
1. Draw the Quadrilateral:
Start by sketching quadrilateral ABCD with AB parallel to CD.
2. Extend Line AB:
Extend line AB to a point E such that line CE is also drawn parallel to line AD.
3. Identify Parallelogram:
Since AB is parallel to CD and AD is parallel to CE, quadrilateral AECD is formed, which is a parallelogram. This is because both pairs of opposite sides are parallel.
4. Use Properties of Parallelograms:
In parallelogram AECD, we know that opposite sides are equal. Thus, AD = CE.
5. Given Condition:
We are given that AD = BC. Therefore, we can conclude that BC = CE.
6. Angles in the Parallelogram:
In parallelogram AECD, the sum of the interior angles on the same side of the transversal (angle A and angle E) is equal to 180 degrees, i.e., angle A + angle E = 180°.
7. Use Alternate Interior Angles:
Since AB is parallel to CD and line AD is a transversal, angle A and angle B are alternate interior angles. Therefore, angle A = angle B.
8. Conclusion:
We have shown that angle A = angle B using the properties of parallelograms and the relationships of angles formed by parallel lines.
Final Statement:
Hence, we have proved that angle A = angle B in quadrilateral ABCD.
---
Start by sketching quadrilateral ABCD with AB parallel to CD.
Extend line AB to a point E such that line CE is also drawn parallel to line AD.
Since AB is parallel to CD and AD is parallel to CE, quadrilateral AECD is formed, which is a parallelogram. This is because both pairs of opposite sides are parallel.
In parallelogram AECD, we know that opposite sides are equal. Thus, AD = CE.
We are given that AD = BC. Therefore, we can conclude that BC = CE.
In parallelogram AECD, the sum of the interior angles on the same side of the transversal (angle A and angle E) is equal to 180 degrees, i.e., angle A + angle E = 180°.
Since AB is parallel to CD and line AD is a transversal, angle A and angle B are alternate interior angles. Therefore, angle A = angle B.
We have shown that angle A = angle B using the properties of parallelograms and the relationships of angles formed by parallel lines.
Hence, we have proved that angle A = angle B in quadrilateral ABCD.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise10videos
STATISTICS
Similar Questions
ABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
View SolutionIn quadrilateral ABCD, AB = AD and BC = CD. Show that ∠ABC=∠ADC.
 View Solution
View SolutionIn quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View SolutionIn cyclic quadrilateral ABCD, AD∣∣BC. Prove that AB = CD.
View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠A=∠B
 View Solution
View SolutionIn a quadrilateral ABCD, AB= AD and CB = CD, prove that AC is perpendicular bisector of BD.
View SolutionIn a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View SolutionIn quadrilateral ABCD, AB||CD and BC||AD. Show that
(i) ΔABD≅ΔCDB
 View Solution
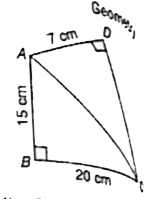
View SolutionIn the given quadrilateral ABCD,AB=15cm,BC=20cmandAD=7cm∠ABC=∠ADC=90∘. Find the length of side CD:
 View Solution
View Solution

