In quadrilateral ABCD, AB||CD and BC||AD. Show that
(i) ΔABD≅ΔCDB

Step by step video & image solution for In quadrilateral ABCD, AB||CD and BC||AD. Show that (i) DeltaABD~=DeltaCDB by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
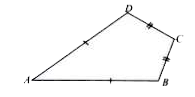
In quadrilateral ABCD, AB = AD and BC = CD. Show that ∠ABC=∠ADC.
 View Solution
View SolutionIn cyclic quadrilateral ABCD, AD∣∣BC. Prove that AB = CD.
View SolutionABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA Prove that (i) ΔABD≅ΔBAC (ii) BD = AC (iii) ∠ABD=∠BAC
View SolutionIn quadrilateral ABCD, AB ||CD and AD= BC, prove that ∠A=∠B.
View SolutionIn the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA.
Prove that (i) ΔABD≅ΔBAC,
(ii) BD = AC,
(iii) ∠ABD=∠BAC.
 View Solution
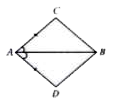
View SolutionIn quadrilateral ABCD, AC=AD and AB bisects ∠A (see figure). Show that ΔABC≅ΔABD. What can you say about BC and BD ?
 View Solution
View SolutionIn quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View SolutionIn a quadrilateral ABCD, AB= AD and CB = CD, prove that AC is perpendicular bisector of BD.
View SolutionIn the given figure, AB||CDandO is the midpoint of AD.
Show that (i) ΔAOB≅ΔDOC.
(ii) O is the midpoint of BC.
 View Solution
View SolutionIn the given figure, AB = CD and AD = CB. Prove that ΔABD≅ΔCDB.
 View Solution
View Solution

