तरंग गति y=asin(kx−ωt) में y प्रदर्शित क्र सकता है
वैघृत क्षेत्र
चुम्बकीये क्षेत्र
विस्थापन
दाब
The correct Answer is:A, B, C, D
ध्वनि तरंगो के लिए y दाब तथा विस्थापन को प्रदर्शित करता है जबकि विघुतचुम्बकीय तरंगो के लिए यह वैघुत अथवा चुम्बकीय क्षेत्रो को प्रदर्शित करता है।
Topper's Solved these Questions
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - सत्य / असत्य
3 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - रिक्त स्थानों की पूर्ति कीजिए
8 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद III )
2 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद iii )
2 Videos
- द्रव्यमान केंद्र और सवेगBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - द्रव्यमान केंद्र और सवेगEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
3 Videos
Similar Questions
समान ताप पर हाइड्रोजन गैस (γ=75) तथा हीलियम गैस (γ=53) में ध्वनि के वेगों का अनुपात √215 है।
View Solutionएक प्रगामी तरंग कि आवृत्ति v तथा कण का विस्थापन - आयाम A है। तरंग के लिए कण का वेग - आयाम . . . . है तथा त्वरण - आयाम . . . . है।
View Solutionअधिकतर पदार्थो का अपवर्तनांक, n>1 होता है। इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम, sinθ1sinθ2=n2n1के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है। लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती। विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक n=(cv)=±√εrμr, होता है, जहाँ C विद्युत – चुम्बकीय तरंगों की निर्यात में चाल तथा v उनकी माध्यम में चाल हैं, εr व μr क्रमशः माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं। आम पदार्थों में εr व μr दोनों धनात्मक होते हैं, अर्थात माध्यम का n धनात्मक है। जब εr व μr दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा। ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-metarial) कहते हैं। वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते। चूँकि n ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है। तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती।
सही प्रकथन चुनें।
View Solutionदर्शाए चित्रानुसार धातु की एक पतली आयताकार पट्टी में एकसमान विद्युत धारा । धनात्मक दिशा में प्रवाहित हो रही है। पट्टी की लम्बाई, चौड़ाई तथा मोटाई क्रमश: 1, wतथा d हैं। पट्टी पर धनात्मक दिशा में एकसमान चुम्बकीय क्षेत्र B लगाया गया हैं। जिसके कारण आवेशवाहक :-दिशा की ओर विक्षेपित होते हैं। परिणामतः सतह PORS पर आवेशवाहकों का संचयन होता है तथा PORS के सामने के फलक पर बराबर किन्तु विपरीत आवेश आ जाता है। तब एक विभवान्तर --दिशा के साथ विकसित होता है। आवेशवाहकों का यह संचयन तब तक जारी रहता है जब तक कि चुम्बकीय बल, वैद्युत बल से सन्तुलित नहीं हो जाता। विद्युत धारा का प्रवाह इलेक्ट्रॉनों के द्वारा तथा पट्टी की अनुप्रस्थ काट पर एकसमान है
Q एक ही चालक पदार्थ की दो अलग-अलग पट्टियों (1 तथा 2) लें। उनकी लम्बाइयाँ बराबर हैं, चौडाइयाँ क्रमश:w1 एवं w2 तथा मोटाइयाँ क्रमश: d1 तथा d2 हैं। दो बिन्दु K तथा Mx-y तल के समान्तर आमने-सामने के फलकों पर स्थित हैं। पट्टियों । तथा 2 में K तथा M के बीच विभवान्तर क्रमश: V1 तथा V2 हैं। तब उनमें बहने वाली एक दी गई विद्युत धारा / तथा एक दी गई चुम्बकीय क्षेत्र की तीव्रता B के लिए सही कथन है (हैं)
View Solutionहर प्रकार की गतिकीय समस्याओं के निश्लेषण के लिए कला-समष्टि चित्रा (Phase space diagrams) का उपयोग किया जाता है। प्रारम्भिक दशा, स्थिति व संवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझने में बहुत उपयोगी है। यहाँ हम एकविमीय सरल गतिकीय निकायों की बात करते हैं। इनके लिए कला-समष्टि समतल है जिसमें स्थिति X-अक्ष पर तथा संबेग Y-अक्ष पर रखते हैं, तब कुला-समष्टि चित्र इस समतल में एक x(t)-p(t) वक्र होगा। वक्र पर तीर समय बढ़ने की दिशा को दर्शाता है।
उदाहरण के लिए, स्थिर वेग से चल रहे कण के लिए कला- समष्टि चित्रा है, सरल रेखा है, जिसे चित्र में दिखाया गया है। चिह्न परिपाटी में स्थिति या संवेग को ऊपर (या दाहिने) ओर धनात्मक तथा नीचे (या बाई) ओर ऋणात्मक माना जाता है।
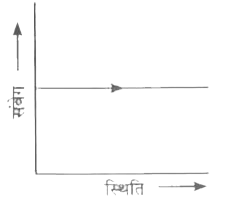
1. जमीन से ऊपर की ओर फेंकी गई गेंद का कला-समष्टि चित्रा है।
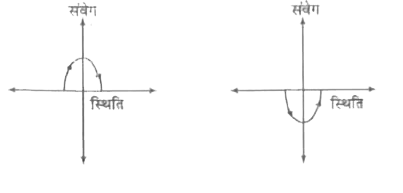
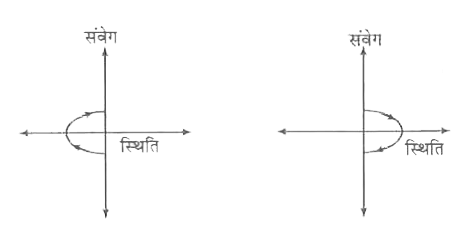
View SolutionIn the relation y=rsin(ωt−kx), the dimensions of ω/k are
View SolutionAssertion: In y = A sin (omega t - kx),(omega t - kx) is dimensionless. Reason: Because dimension of omega = [M^(0)L^(0)T] .
View SolutionIn a wave motion y=sin(kx−ωt),y can represent :-
View SolutionThe stationary wavey=2asinkxcosωt in a closed organ pipe is the result of the superposition of y=asin(ωt−kx)
View SolutionWhich two of the following waves are in the same phase?
y=Asin(kx−ωt)
y=Asin(kx−ωt+π)
y=Asin(kx−ωt+π/2)
y=Asin(kx−ωt+2π)
View Solutionअप्रगामी तरंग y=2asinkxcosωt , बन्द आर्गन पाइप में y=asin(ωt–kx) तथा ........ के अध्यारोपण से बनती है।
View SolutionA travelling wave represented by y = A sin (omega t - kx) is superimposed on another wave represented by y = A sin (omega t + kx). the resultant is :
View Solutionthe equation y=alpha sin(omega t+kx) In omega Is the dimensional formula of
View Solutiony(x,t)=asin(kx−ωt) द्वारा निरूपित गतिमान तरंग, y(x,t)=asin(kx+ωt) द्वारा निरूपित अन्य तरंग पर अध्यारोपित होती है। परिणामी होगा
View SolutionIn a wave motion y = a sin(kx - omega t) , y cen represent
View Solution
