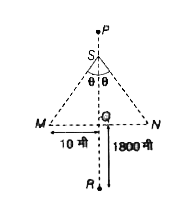
दो लाउडस्पीकर M एवं N जो की एक दूसरे से 20m की दूरी पर है, क्रमशः 118 Hz एवं 121 Hz की ध्वनि उत्सर्जित करते हैं। बिन्दु P रेखा MN के द्विभाजक लम्ब पर स्थित है तथा MN के मध्य बिन्दु Q से 1800 m की दूरी पर है। एक कार बिन्दु P से बिन्दु Q की तरफ 60km/hr की स्थित गति से चलना प्रारम्भ करती है। कार Q बिन्दु को पार कर अंततोगत्वा बिन्दु R के आगे चली जाती है, जहाँ बिन्दु R बिन्दु Q से 1800m की दूरी पर है । कार में बैठा व्यक्ति समय t पर विस्पंद-आवृत्ति (beat frequency) v(t ) मापता है । बिन्दु P, Q, R पर विस्पंद - आवृती क्रमश: vp,vQ,vR है । ध्वनि की हवा में गति 330ms−1 है। कार में बैठे व्यक्ति द्वारा सुनी गयी ध्वनि के बारे में निम्नलिखित में से कौनसा/कौनसे कथन सत्य है/ है ?
नीचे दिखाया गया लेखाचित्र विस्पन्द आवृत्ति का समय के साथ परिवर्तन की व्यवस्था को दर्शाता हैं
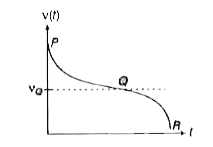
जब कार Q बिन्दु को पार करती हैं , विस्पन्द आवृत्ति की दर में अधिकतम परिवर्तन होता हैं
VP+VR=2VQ
नीचे दिखाया गया लेखाचित्र विस्पन्द आवृत्ति का समय के साथ परिवर्तन की व्यवस्था को दर्शाता हैं

The correct Answer is:B, C, D
कार की चाल, v = 60 किमी / घण्टा =60×518 मी / से =5003 मी / से
P तथा Q के बीच बिन्दु S पर
vM=vM(C+vcosθC)
vN=vN(C+vcosθC)
⇒Δv=(vN~vM)(1+vcosθC)
इसी प्रकार Q तथा R के बीच,
Δ=(vN−vM)(1+vcosθC)
⇒d(Δv)dt=±(vN−vM)vCsinθdθdt
बिन्दु P तथा R जोकि M तथा N से , पर θ=0∘ अधिक दुरी पर है।
∴ P तथा R के लिए , ग्राफ का ढाल शून्य होगा। बिन्दु Q पर θ=90∘sinθ अधिकतम है तथा dθdt का मान भी अधिकतम है।
[ ∵dthηdt=vr , जहाँ v वेग है तथा r, P तथा S के बीच की लम्बाई है तथा r का मान Q पर न्यूनतम है। ]
अतः बिन्दु Q पर ढाल का मान अधिकतम है।
बिन्दु P पर, vP=Δv=(vN−vM)(1+vC) (∵θ=0∘)
बिन्दु R पर, vR=Δv=(vN−vM)(1−vC) (∵θ=0∘)
बिन्दु Q पर, vQ=Δv=(vN−vM) (∵θ=90∘)
इन समीकरणों के द्वारा हमें ज्ञात होता है।
vP=VR=2vQ
Topper's Solved these Questions
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - सत्य / असत्य
3 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - रिक्त स्थानों की पूर्ति कीजिए
8 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद III )
2 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद iii )
2 Videos
- द्रव्यमान केंद्र और सवेगBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - द्रव्यमान केंद्र और सवेगEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
3 Videos
Similar Questions
समान ताप पर हाइड्रोजन गैस (γ=75) तथा हीलियम गैस (γ=53) में ध्वनि के वेगों का अनुपात √215 है।
View Solutionएक प्रगामी तरंग कि आवृत्ति v तथा कण का विस्थापन - आयाम A है। तरंग के लिए कण का वेग - आयाम . . . . है तथा त्वरण - आयाम . . . . है।
View Solutionअधिकतर पदार्थो का अपवर्तनांक, n>1 होता है। इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम, sinθ1sinθ2=n2n1के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है। लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती। विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक n=(cv)=±√εrμr, होता है, जहाँ C विद्युत – चुम्बकीय तरंगों की निर्यात में चाल तथा v उनकी माध्यम में चाल हैं, εr व μr क्रमशः माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं। आम पदार्थों में εr व μr दोनों धनात्मक होते हैं, अर्थात माध्यम का n धनात्मक है। जब εr व μr दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा। ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-metarial) कहते हैं। वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते। चूँकि n ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है। तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती।
सही प्रकथन चुनें।
View Solutionदर्शाए चित्रानुसार धातु की एक पतली आयताकार पट्टी में एकसमान विद्युत धारा । धनात्मक दिशा में प्रवाहित हो रही है। पट्टी की लम्बाई, चौड़ाई तथा मोटाई क्रमश: 1, wतथा d हैं। पट्टी पर धनात्मक दिशा में एकसमान चुम्बकीय क्षेत्र B लगाया गया हैं। जिसके कारण आवेशवाहक :-दिशा की ओर विक्षेपित होते हैं। परिणामतः सतह PORS पर आवेशवाहकों का संचयन होता है तथा PORS के सामने के फलक पर बराबर किन्तु विपरीत आवेश आ जाता है। तब एक विभवान्तर --दिशा के साथ विकसित होता है। आवेशवाहकों का यह संचयन तब तक जारी रहता है जब तक कि चुम्बकीय बल, वैद्युत बल से सन्तुलित नहीं हो जाता। विद्युत धारा का प्रवाह इलेक्ट्रॉनों के द्वारा तथा पट्टी की अनुप्रस्थ काट पर एकसमान है
Q एक ही चालक पदार्थ की दो अलग-अलग पट्टियों (1 तथा 2) लें। उनकी लम्बाइयाँ बराबर हैं, चौडाइयाँ क्रमश:w1 एवं w2 तथा मोटाइयाँ क्रमश: d1 तथा d2 हैं। दो बिन्दु K तथा Mx-y तल के समान्तर आमने-सामने के फलकों पर स्थित हैं। पट्टियों । तथा 2 में K तथा M के बीच विभवान्तर क्रमश: V1 तथा V2 हैं। तब उनमें बहने वाली एक दी गई विद्युत धारा / तथा एक दी गई चुम्बकीय क्षेत्र की तीव्रता B के लिए सही कथन है (हैं)
View Solutionहर प्रकार की गतिकीय समस्याओं के निश्लेषण के लिए कला-समष्टि चित्रा (Phase space diagrams) का उपयोग किया जाता है। प्रारम्भिक दशा, स्थिति व संवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझने में बहुत उपयोगी है। यहाँ हम एकविमीय सरल गतिकीय निकायों की बात करते हैं। इनके लिए कला-समष्टि समतल है जिसमें स्थिति X-अक्ष पर तथा संबेग Y-अक्ष पर रखते हैं, तब कुला-समष्टि चित्र इस समतल में एक x(t)-p(t) वक्र होगा। वक्र पर तीर समय बढ़ने की दिशा को दर्शाता है।
उदाहरण के लिए, स्थिर वेग से चल रहे कण के लिए कला- समष्टि चित्रा है, सरल रेखा है, जिसे चित्र में दिखाया गया है। चिह्न परिपाटी में स्थिति या संवेग को ऊपर (या दाहिने) ओर धनात्मक तथा नीचे (या बाई) ओर ऋणात्मक माना जाता है।
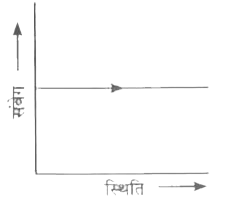
1. जमीन से ऊपर की ओर फेंकी गई गेंद का कला-समष्टि चित्रा है।
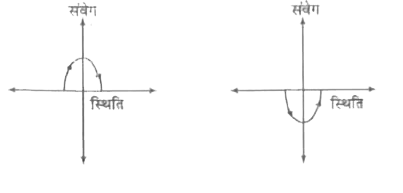
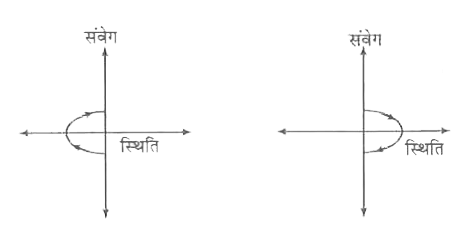
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionपरवलय y2=36x पर स्थित वे बिन्दु जिनकी कोटि भुज की तिगुनी है, हैं
View Solutionरिक्त स्थानों की पूर्ति कीजिए -
मूल बिन्दु 0 से समतल →r.→N=d की दूरी ............... है।
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solutionएक बिन्दु की रेखा से दूरी |महत्वपूर्ण प्रश्न
View Solutionएक बिन्दु की रेखा से लम्बवत दूरी |दो समांतर रेखाओ के मध्य दूरी
View Solutionसरल रेखाएँ|एक बिन्दु की रेखा से दूरी#!#दो समांतर रेखाओ के बीच की दूरी#!#प्रश्नो पर चर्चा
View Solution
