A(3,2,0),B(5,3,2) and C(−9,6,−3) are the vertices of a triangle ABC if bisector of angle BAC meets BC at D, then co-ordinates of D are
Video Solution
Text Solution
The correct Answer is:N/a
AB=√(5−3)2+(3−2)2+(2−0)2
=√4+1+4=3
AC=√(−9−3)2+(6−2)2+(−3−0)2
=√144+16+9=13
AD is the bisector of ∠A.
∴BDDC=ABAC=313
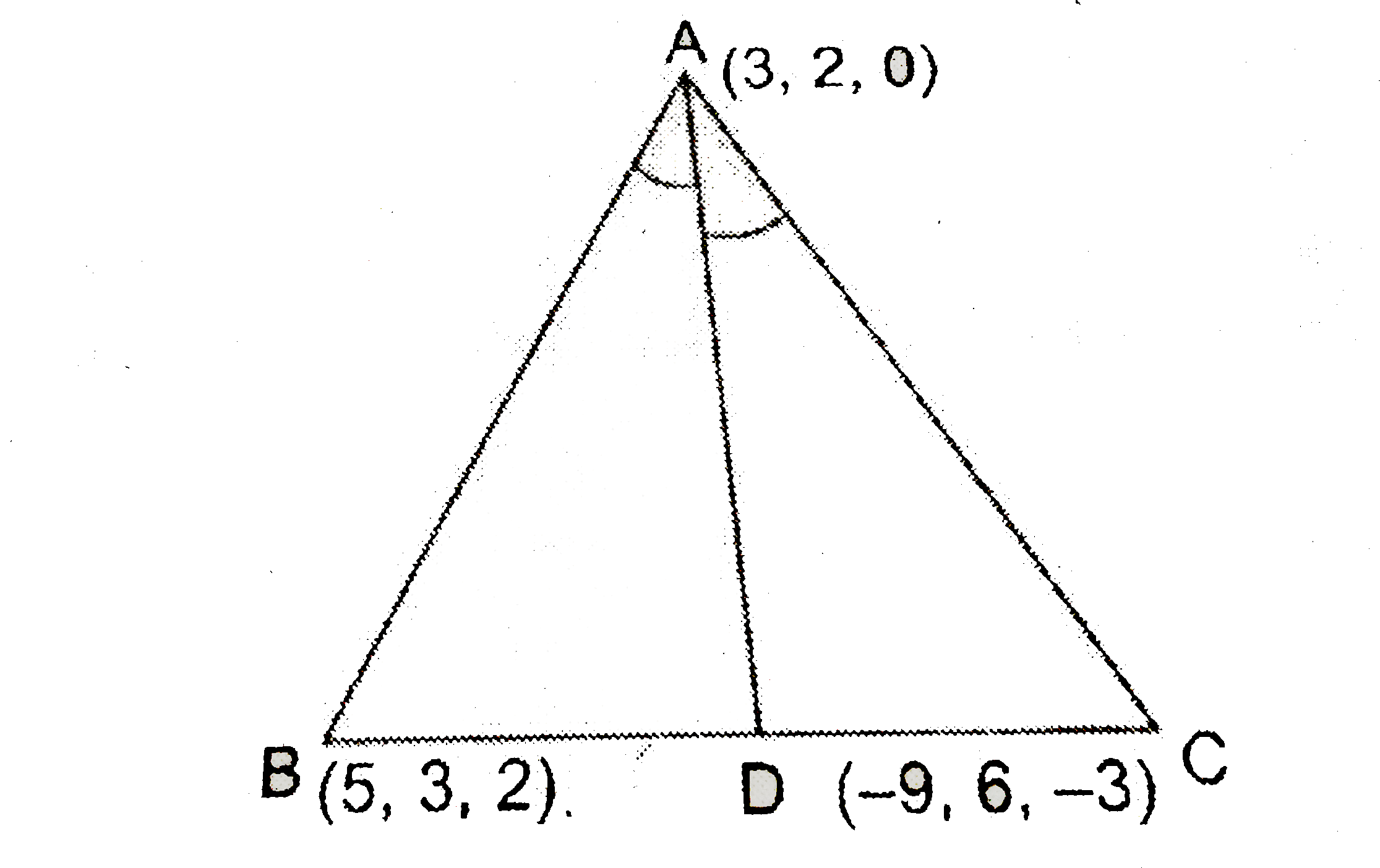
i.e., D divides BC in the ratio 3 : 13.
∴ Co-ordinates of D
(3×(−9)+13×53+13,3×6+13×33+13,3×(−3)+13×23+13)
=(3816,5716,1716)=(198,5716,1716)
|
Topper's Solved these Questions
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Exercise 12 A
5 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Exercise 12 B
18 Videos
- CONIC SECTIONBOOK - NAGEEN PRAKASHANCHAPTER - CONIC SECTIONEXERCISE - Miscellaneous Exercise
8 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise
30 Videos
Similar Questions
Knowledge Check
A(3,2,0),B(5,3,2)andC(−9,8,−10) are the vertices of a triangle ABC. If the bisector of ∠ABC meets BC atD, then coordinates of D are
A(198,5716,1716)B(−198,5716,1716)C(198,−5716,1716)DNone of theseA(3,2,0),B(5,3,2),C(−9,6,−3) are the vertices of a triangle ABC. If the bisector of ∠BAC meets BC at D, then coordinates of D are
A(198,5716,1716)B(−198,5716,1716)C(198,−5716,1716)D(198,5716,−1716)If A (3, 2, 0), B (5, 3, 2) and C (-9, 6, -3 ) are three points forming a triangle and AD is bisector of ∠BAC, then AD meets BC at the point
A(19,8,5716,1716)B(−198,5716,1716)C(198,5716,17,16)Dnone of these
A(−1,2,−3),B(5,0,−6)andC(0,4,−7)are the vertices of a triangle. The DRs of the internal bisector of ∠BAC are
View SolutionA(3,2,0),B(5,3,2),(−9,6,−3) are the vertices of △ABC and AD is the bisector of ∠BAC which meets at D. Find the coordinates of D,
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionLet A(3,2,0),B(5,3,2)C(−9,6,−3) be three points forming atriangle. AD, the bisector of ∠BAC, meets BC in D. Find thecoordinates of the point D.
View SolutionIn the triangle ABC, vertices A, B, C are (1,2),(3,1),(−1,6) respectively. If the internal angle bisector of ∠BAC meets BC at D, then the coordinates of D are (53,83)
View Solution
