Let ABCD be a trapezium with parallel sides AB and CD such that the circle S with AB as its diameter touches CD. Further, the circle S passes through the midpoints of the diagonals AC and BD of the trapezium. The smallest angle of the trapezium is
A
π3
B
π4
C
π5
D
π6
Text Solution
The correct Answer is:D
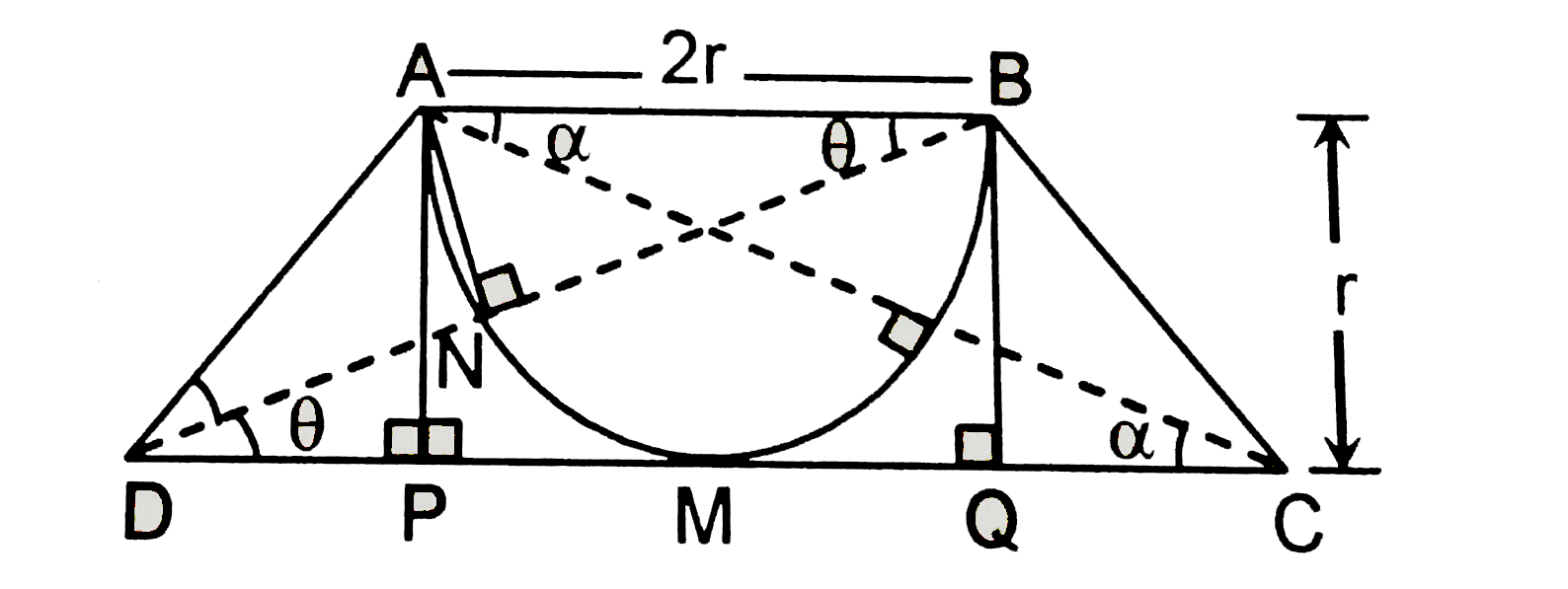
Join AN
∵∠ANB=90∘
In △ANB,
cos θ=BQ2r
BN=2rcos θ
BD=2BN=4rcos θ
In △BQD
sin θ=BQBD=r4r cos θ
sin 2θ=12
θ=15∘
Now similarly α=15∘=θ & AC=4rcos α
∴ Trapezium will be isosceles
∵∠ADB=30∘
|
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Matematics
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 1 Mathematics
45 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHMATICS
10 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium with ∠A=90∘andAB parallel to CD. Then ∠B is :
A90∘B90∘−∠CC360∘−∠CD180∘−∠CABCD is a trapezium with ∠A=90∘andAB parallel to CD. Then ∠B is :
A90∘B90∘−∠CC360∘−∠CD180∘−∠CLet ABCD be a trapezium ,in which AB is parallel to CD, AB =11 ,BC=4,CD=6 and DA=3. the distance between AB and CD is
A2B2.4C2.8Dnot determinable with the data
ABCD is a trapezium in which AB∣∣CD then AC2+BD2 is equal to
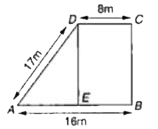
View SolutionIn the given figure , ABCD is a trapezium in which the parallel sides AB,CD are both perpendicular to BC. Find the area of the trapezium :
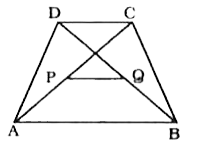
View SolutionIn trapezium ABCD,AB∣∣CDwith AB=24cm.andCD=16cm. P and Q are mid-points of the diagonals AC and BD respectively. Find the length of PQ.
View SolutionSuppose ABCD is a trapezium whose sides and height are integers and AB is parallel to CD. If the area of ABCD is 12 and the sides are distinct, then |AB-CD|
View SolutionABCD is a trapezium in which AB is parallel to CD and AB = 4 (CD). The diagonals of the trapezium intersects at O. What is the ratio of area of triangle DCO to the area of the triangle ABO?
View Solution
